Approximation et extrapolation par moindres carrés

Approximation et extrapolation par moindres carrés#

Approximation par moindres carrés#

\[ \theta = (H^TH)^{-1} H^Ty \]
# Normalisation des abscisses entre 0 et 1
x = (year-1880) / (2020-1880)

# Données sous forme de vecteur colonne
y = np.transpose(temp)

# Matrice H
H = np.transpose(np.array([ x**0, x**1, x**2 ]))

# Estimation des paramètres θ
HT     = np.transpose(H)
HTH    = np.dot(HT, H)
HTHinv = linalg.pinv(HTH)
HTy    = np.dot(HT, y)
theta  = np.dot(HTHinv, HTy)

print(theta)

# Calcul du polynôme z
z = np.dot(H,theta)

[-0.20093458 -0.67671687  1.75631332]
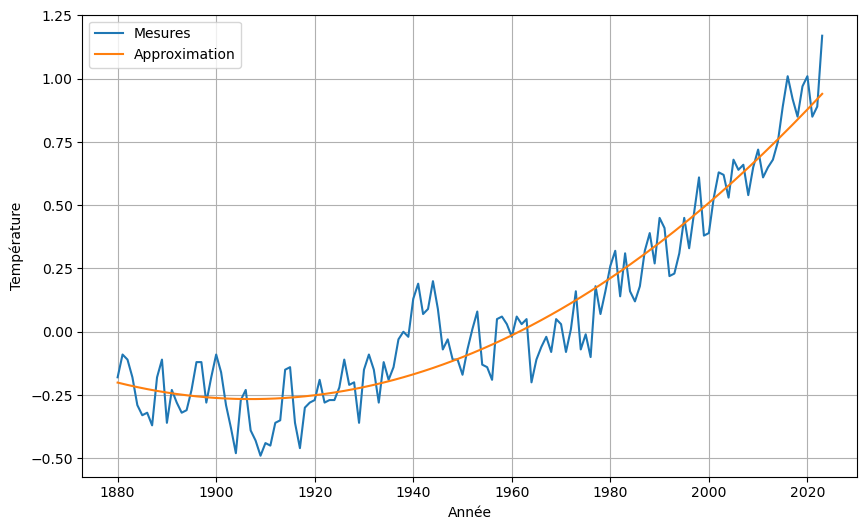
../_images/83d3a167215c3d31c953a8ca07136e4e762879d141cb1585de2fa17162fe79a9.png

Extrapolation#

Pour extrapoler la courbe (c’est-à-dire calculer ses valeurs au délà des données), il suffit de calculer le polynôme sur une autre plage des abscisses, donc en redéfinissant \(H\).

year2 = np.arange(1880,2070)
x = (year2-1880)/(2020-1880)
H = np.transpose(np.array([ x**0, x**1, x**2 ]))
z = np.dot(H,theta)
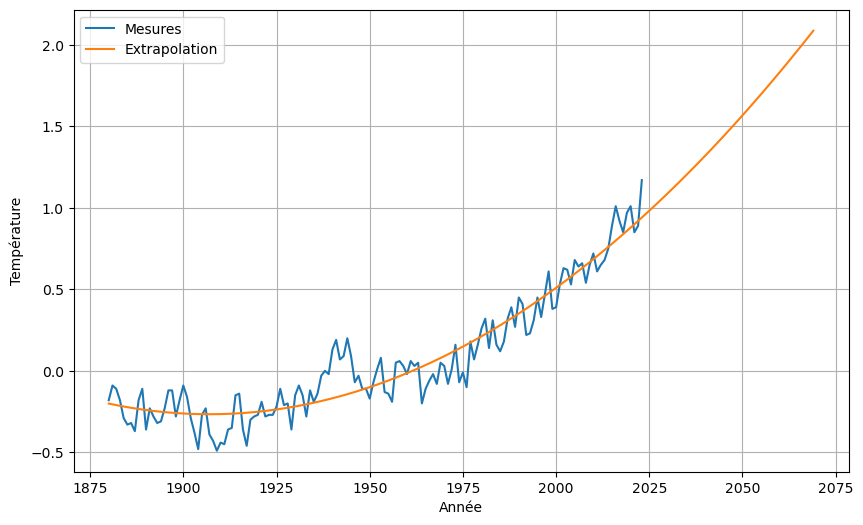
../_images/40f397adca1d0a8f7639194db42fb4633ab389a16628a7d194f306efeef26aff.png

Si vous avez le moral accroché, vous pouvez connaître les conséquences issues de cette extrapolation sur l’article Wikipedia Changement climatique… 😱

Données :

Contenu