Démodulation d’un message numérique modulé en bande de base#
Émetteur#
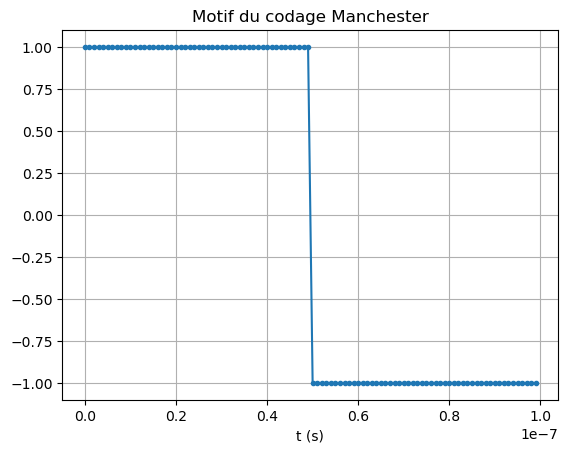
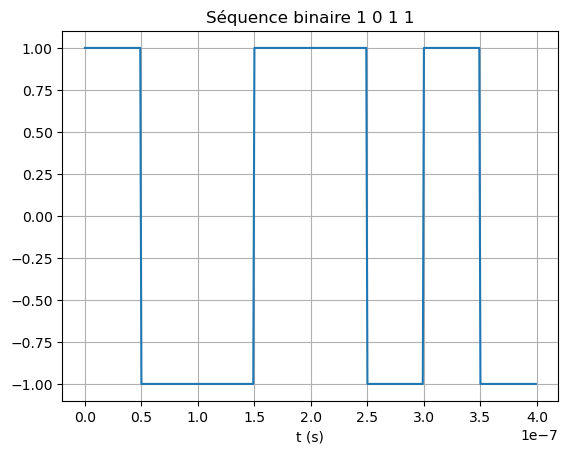
Canal de transmission#
# Bruit gaussien
snr = -10
N = len(x)
Px = np.linalg.norm(x)**2/N
sig = np.sqrt(Px * 10**(-snr/10))
b = np.random.normal(0, sig, N)
y = x + b
Récepteur#
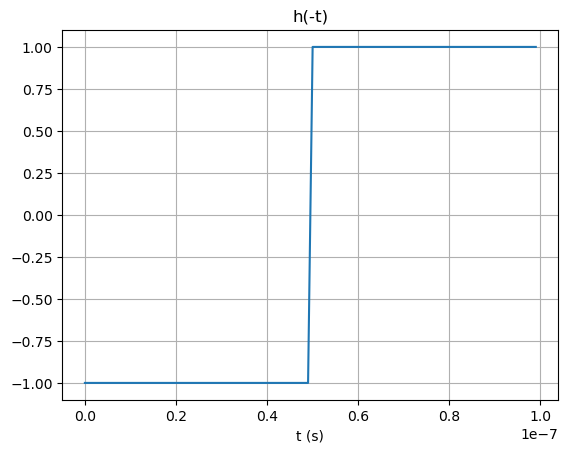
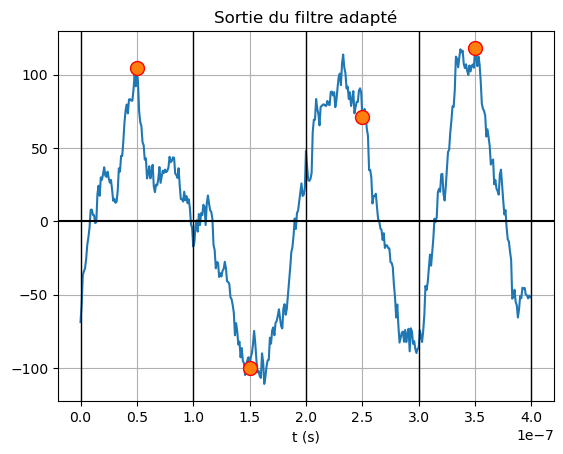
# Réponse impulsionnelle du filtre adapté
h = motif[::-1]
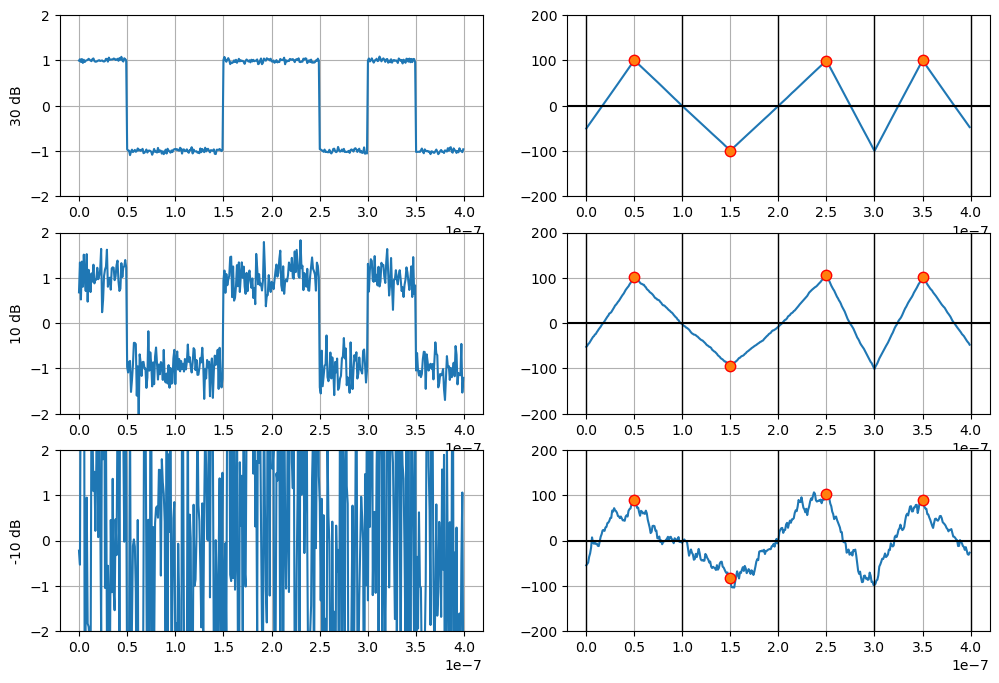
Robustesse par rapport au bruit#
L’exemple ci-dessus est reproduit pour différents RSB.
On peut approfondir l’étude en testant un grand nombre de RSB, et pour chacun d’eux calculer le nombre d’erreurs de transmission, c’est-à-dire le nombre de bits différents entre la séquence binaire émise et la séquence binaire identifiée par le récepteur.
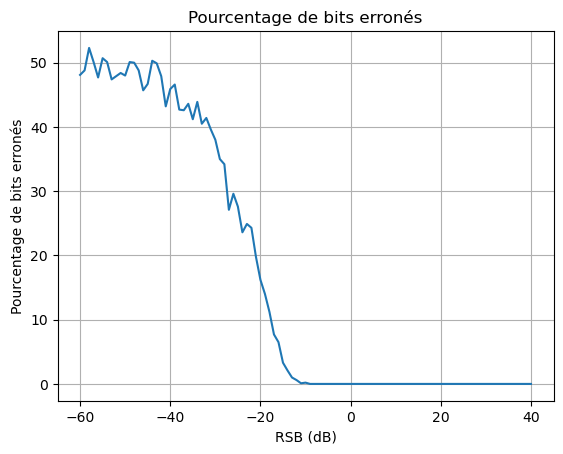
Comme on pouvait s’y attendre, le nombre d’erreur diminue lorsque le RSB augmente.
On remarque par ailleurs que si le RSB est supérieur à \(-10\) dB, il n’y a aucune erreur détectée, ce qui montre que le filtre adapté est une méthode très robuste au bruit !
Il y a une stagnation du pourcentage d’erreurs à environ 50 % pour un RSB inférieur à \(-40\) dB : dans ces conditions, le bruit est tellement fort que le filtre adapté se comporte comme un générateur aléatoire indépendant du message émis.
Décodage du signal manchester.csv#
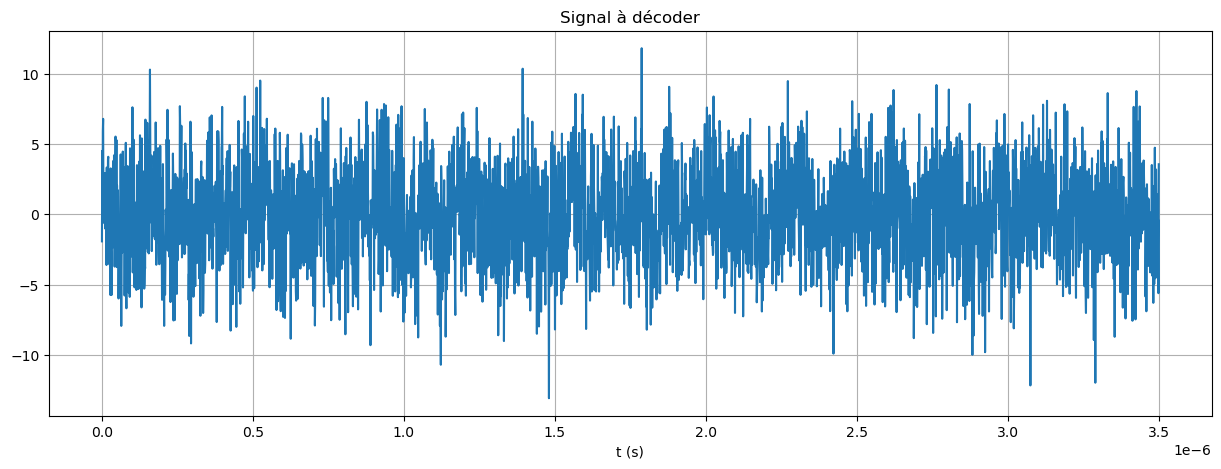
La séquence décodée est :
[1 0 0 0 0 1 0 1 0 1 0 0 1 0 1 0 0 0 0 0 1 1 0 1 0 1 1 0 1 0 0 1 1 1 1]
Ce qui, en regroupant les bits 7 par 7 (code ASCII) permet d’obtenir le message :
BRAVO