Exercices sur feuille#
Système linéaire invariant#
Exercice 1#
Dans le cas de signaux à temps discrets, montrez que la sortie d’un système linéaire invariant s’exprime comme la convolution de l’entrée par la réponse impulsionnelle du système. Pour cela, utilisez le fait que l’entrée peut s’écrire comme une somme d’impulsions.
Exercice 2#
Représentez la réponse fréquentielle d’un système de réponse impulsionnelle
Conception d’un gabarit#
Exercice 3#
Représentez le gabarit d’un filtre passe-bas de largeur de transition 20 Hz, de bande passante 100 Hz, d’ondulation maximale en bande passante 1 dB et d’atténuation minimale 30 dB.
Exercice 4#
Représentez le gabarit d’un filtre numérique qui atténue d’au moins 60 dB les fréquences inférieures à 10 kHz et d’au plus 3 dB les fréquences supérieures à 15 kHz. La fréquence d’échantillonnage est de 100 kHz.
Exercice 5#
La capture d’écran ci-dessous est tirée de l’outil de conception de filtres analogiques d’Analog Devices. Représentez le gabarit correspondant.

Exercice 6#
Kévin, un ancien étudiant en FIP, a effectué son projet de fin d’études sur l’imagerie des particules magnétiques. Le principe est de mesurer la réponse de particules super-paramagnétiques à un champ magnétique oscillant de fréquence 25 kHz. Le signal mesuré en réponse à cette excitation contient, en plus de la fréquence excitatrice, des harmoniques de 50 kHz et plus. On considère qu’au-delà de 2 MHz, l’amplitude du signal est trop faible pour pouvoir être détectée. Le signal d’intérêt qui permet de construire une image de l’objet étudié correspond aux harmoniques. Le filtre doit répondre à des critères supplémentaires :
atténuation maximale de 3 dB dans la bande passante ;
atténuation minimale de 60 dB ;
le filtrage ne doit pas générer de perturbation.
Proposez le gabarit permettant de concevoir le filtre qui sélectionnera le signal d’intérêt.
Transformées de Laplace et en Z#
Exercice 7#
Pour chacun des diagrammes pôles-zéros ci-dessous :
donnez les pôles et zéros,
précisez l’ordre du système,
indiquez si ces systèmes sont analogiques ou numériques.
Exercice 8#
On considère les deux filtres analogiques de réponses impulsionnelles :
Pour chacun d’eux :
Calculez la transformée de Laplace.
Représentez la région de convergence.
Placez les pôles et zéros.
Ce filtre est-il stable ?
Exercice 9#
On considère les deux filtres numériques de réponses impulsionnelles :
Pour chacun d’eux :
Calculez la transformée en Z.
Représentez la région de convergence.
Placez les pôles et zéros.
Ce filtre est-il stable ?
Exercice 10#
Calculez les transformées de Laplace inverse de :
Exercice 11#
Calculez les transformées en Z inverse de :
Exercice 12#
Deux filtres \(H_1(s)\) et \(H_2(s)\) sont mis en série. Leurs fonctions de transfert sont :
Quel est l’ordre de chacun de ces deux filtres ?
Quelle est la fonction de transfert du filtre global \(H(s)\) ? Quel est son ordre ?
Qu’obtient-on en ajoutant un troisième filtre du premier ordre à \(H(s)\) ?
Filtres numériques#
Exercice 13#
Montrez que le filtre de fonction de transfert
peut se représenter sous la forme directe 1 ci-dessous :
Pour cela, écrivez \(y[n]\) en fonction de \(x[n]\), puis utilisez la transformée en Z pour obtenir l’expression de \(H(s)\).
Exercice 14#
On souhaite réaliser avec la méthode des fenêtres un filtre numérique passe-bas de bande passante 20 Hz et de bande de transition 10 Hz. Les atténuations limites des bandes passante et atténuée sont respectivement de 0,1 dB et 40 dB. La fréquence d’échantillonnage est égale à 120 Hz
Représentez le gabarit.
Que peut-on dire de sa stabilité ?
Quelles fenêtres peuvent être utilisées pour obtenir un filtre vérifiant le gabarit ?
Parmi celles-ci, quelle fenêtre donnera l’ordre le plus faible ? Calculez son ordre.
Exercice 15#
Montrez que le filtre de fonction de transfert
peut se représenter sous la forme directe 1 ci-dessous :
Exercice 16#
On souhaite réaliser avec la transformation bilinéaire un filtre numérique passe-bas de bande passante 30 Hz et de bande de transition 60 Hz. Les atténuations limites des bandes passante et atténuée sont respectivement de 1 dB et 15 dB. La fréquence d’échantillonnage est égale à 500 Hz
Représentez le gabarit.
Que peut-on dire de sa stabilité ?
Représentez le gabarit du filtre analogique.
Le filtre analogique synthétisé à partir du gabarit précédent a pour fonction de transfert
Donnez la fonction de transfert du filtre numérique.
Exercice 17#
Représentez la forme directe 1 de la fonction de transfert :
Exercice 18#
Déterminez les fonctions de transfert des formes directes ci-dessous, puis calculez leur réponse impulsionnelle.
Filtres analogiques#
Exercice 19#
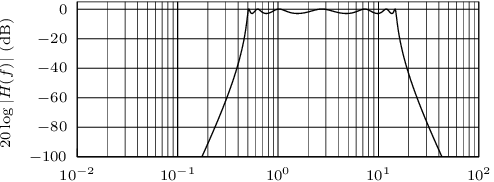
Identifiez le type de filtre correspondant à la réponse fréquentielle ci-dessous. Précisez également la bande passante du filtre (les fréquences sont données en hertz).
Exercice 20#
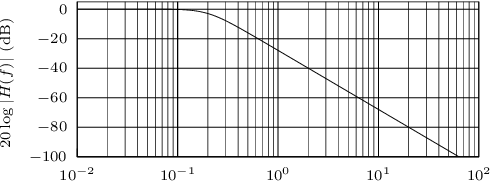
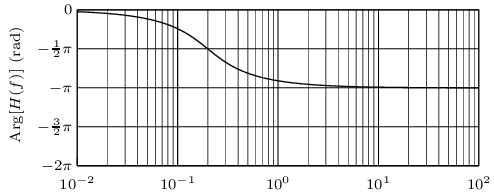
Identifiez le type de filtre correspondant à la réponse fréquentielle ci-dessous. Précisez également la bande passante du filtre (les fréquences sont données en hertz).