Produit de convolution

Génération des signaux avec la fonction numpy.where. Il est utile de définir au préalable un tableau contenant les abscisses.

# Abscisses de -10 à 10 (penser à rajouter +1 à la limite de droite)
n = np.arange(-10, 10+1)

# Signal x
x = np.where( n==1, 1, 0) + np.where( n==-1, -1, 0)

# Signal y
y = np.where( abs(n)<=1, 2, 0)

On affiche les signaux pour vérifier qu’ils sont bien construits…

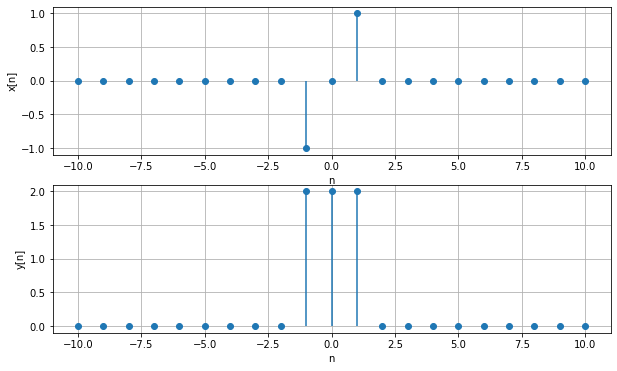
La convolution est obtenue avec numpy.convolve. Attention à bien choisir la valeur du troisième paramètre (mode) !

z = np.convolve(x, y, "same")

Résultat :

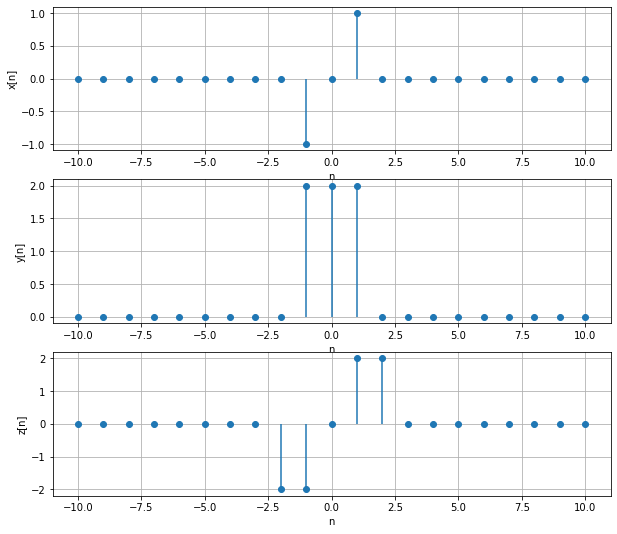
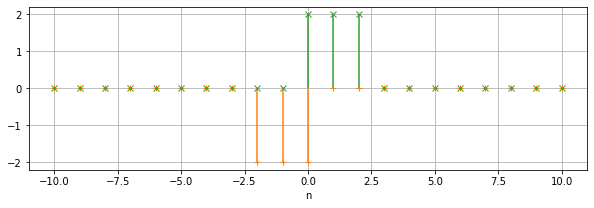
Le résultat obtenu peut s’interpréter comme la somme des deux signaux ci-dessous, chacun d’eux étant la convolution de \(y\) avec l’une des deux impulsions de \(x\) : l’impulsion en \(-1\) donne le signal orange et l’impulsion en \(+1\) donne le signal vert.