Transformée de Fourier discrète#
Importation des modules…
import numpy as np
import matplotlib.pyplot as plt
import scipy.fft as fft
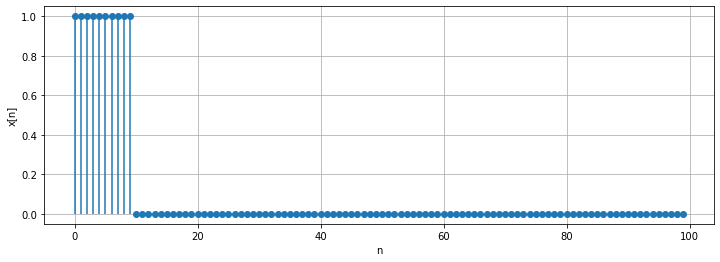
Après avoir importé les modules nécessaires, le créneau est généré sur \(N=\) 100 échantillons. Attention, les 10 premiers échantillons (de 0 à 9) sont égaux à 1, les suivants (de 10 à 99) sont nuls !
N = 100
n = np.arange(N)
x = np.where(n<10, 1, 0)
On peut vérifier certaines valeurs (l’échantillon \(-1\) correspond au dernier échantillon) :
for m in [0, 9, 10, -1]:
print(f"x[{m}] = {x[m]}")
x[0] = 1
x[9] = 1
x[10] = 0
x[-1] = 0
Un conseil, affichez le signal pour vérifier qu’il est bien construit !
plt.figure(figsize=(12,4))
plt.stem(n, x, basefmt=" ")
plt.xlabel("n")
plt.ylabel("x[n]")
plt.grid()
plt.show()
TFD entre \(0\) et \(N-1\)#
FFT est un algorithme très rapide pour calculer une transformée de Fourier discrète (TFD).
Il est implémenté en Python dans scipy.fft.fft.
Par défaut, FFT calcule une TFD entre \(0\) et \(N-1\).
Pour la représenter, il faut donc définir les abscisses \(k\) entre \(0\) et \(N-1\).
k = np.arange(N)
X = fft.fft(x)
N’oubliez pas : la TFD est très souvent complexe, c’est pourquoi on la représente avec deux graphes : le module et l’argument.
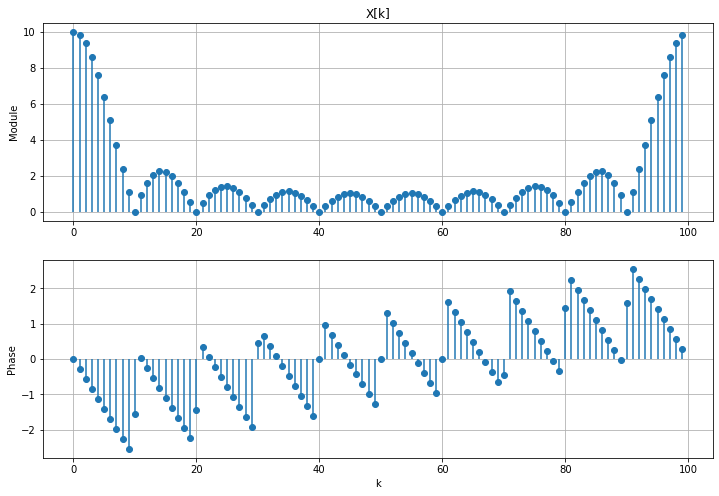
Dans certains cas, il peut y avoir des impulsions bizarres sur la phase : ce sont des erreurs numériques que l’on peut supprimer en forçant à 0 les échantillons de \(X\) qui sont très faibles :
X[abs(X)<1e-9] = 0
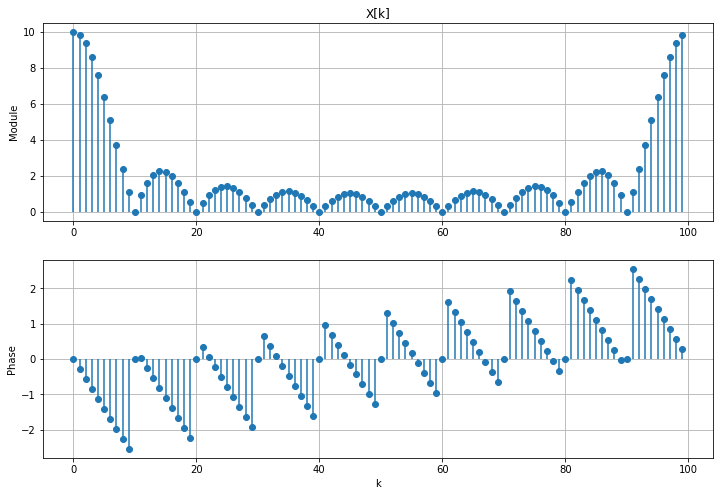
Le signal temporel étant un créneau, on peut l’interpréter comme un signal porte périodisé. Par conséquent, le module de son spectre est bien la TFD d’une porte (un sinus cardinal) périodisé.
TFD entre \(-N/2\) et \(N/2-1\)#
Il suffit de redéfinir les abscisses, et d’appliquer scipy.fft.fftshift sur le spectre pour inverser les parties gauche et droite.
k = np.arange(-N/2, N/2)
X = fft.fftshift(X)
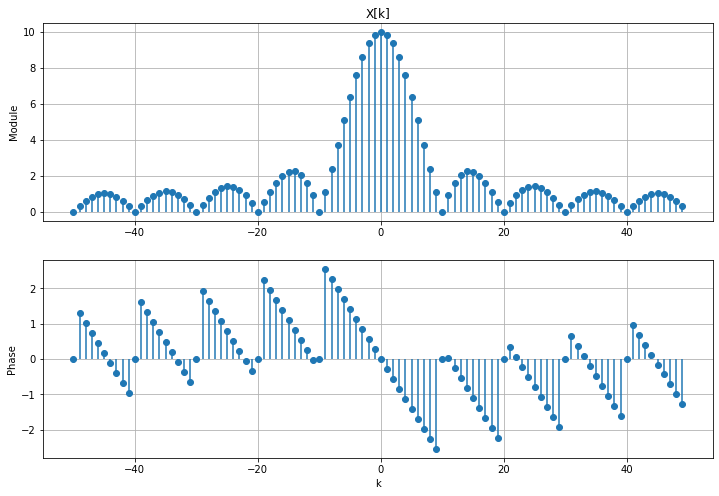
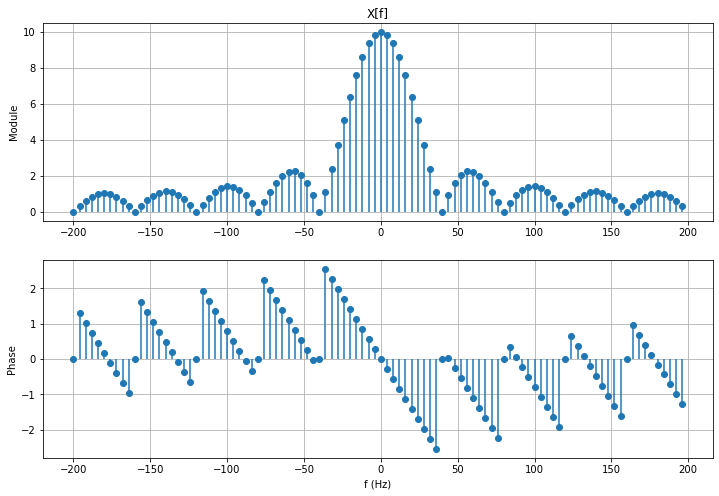
TFD centrée en fonction des fréquences#
Dans ce cas, le module et la phase du spectre ne changent pas. Seule l’abscisse est à redéfinir.
Te = 2.5e-3
fe = 1/Te
f = k*fe/N