Corrections

Système linéaire invariant

Exercice 1

La réponse impulsionnelle \(h\) d’un système linéaire invariant est par définition la sortie de ce système à une impulsion. Par ailleurs, si l’entrée \(x\) du système est un signal échantillonné alors elle peut s’écrire comme une somme d’impulsions :

\[ x[n] = \sum_{m} x[m] \delta[n-m]. \]

Ainsi, en notant \(\mathcal{S}\) l’effet du système, sa sortie a pour expression :

\[\begin{split} y[n] &= \mathcal{S}\left(x[n]\right) \\ &= \mathcal{S}\left(\sum_{m} x[m] \delta[n-m]\right) \\ &= \sum_{m} \mathcal{S}(x[m] \delta[n-m]) &&\text{(par linéarité)} \\ &= \sum_{m} x[m] \mathcal{S}(\delta[n-m]) &&\text{(par linéarité, $x[m]$ étant une constante)} \\ &= \sum_{m} x[m] h[n-m] &&\text{(par invariance)} \\ &= (x*h)[n] \\ \end{split}\]

Exercice 2

La réponse fréquentielle du système de réponse impulsionnelle \(h\), qui s’obtient en calculant la transformée de Fourier, est :

\[ H(f) = \frac{1}{1+j2\pi f} \]

dont on peut déduire le gain et la phase :

\[ 20\log_{10}|H(f)| = -10\log_{10}\left(1+4\pi^2 f^2\right) \qquad \mathrm{Arg}(H(f)) = \mathrm{arctan}(-2\pi f). \]

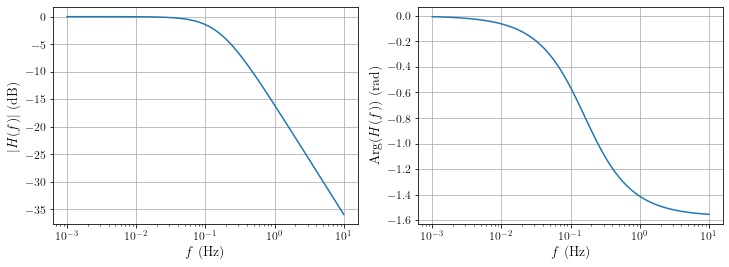
Conception d’un gabarit

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Les spécifications du filtre à mettre en place ne sont données que pour certaines plages de fréquences. Nous choisissons de réaliser un filtre passe-haut (plutôt qu’un filtre passe-bande par exemple) afin de minimiser l’ordre du filtre réalisé. Les lignes en tirets sont des choix effectués pour obtenir le gabarit d’un filtre passe-haut.

Transformées de Laplace et en Z

Exercice 7

L’ordre correspond au nombre de pôles. Le type (analogique ou numérique) se voit grâce au lieu de la transformée de Fourier (continue ou discrète) : une barre verticale sur l’axe des ordonnées correspond à un système analogique, le cercle unité correspond à un système numérique.

	Pôles	Zéros	Ordre	Type
A	\(-3-4j\) \(-3+4j\)	Aucun zéro	\(2\)	Analogique
B	\(-\frac{1}{2}j\) \(+\frac{1}{2}j\)	\(-2\)	\(2\)	Numérique
C	\(0,81+1,05j\) \(0,81-1,05j\) \(-0,25+0,48j\) \(-0,25-0,48j\) \(-1,11\)	\(0,18+0,86j\) \(0,18-0,86j\) \(-0,43\) \(-6\)	\(5\)	Numérique

Exercice 8

Le calcul de la transformée de Laplace peut nécessiter de calculer la limite en \(t \to +\infty\) d’une exponentielle. Dans ce cas, il faut séparer l’exponentielle en deux :

• une exponentielle réelle qui va converger vers 0 selon certaines valeurs de la partie réelle \(\sigma\) de \(s\) ;

• une exponentielle complexe qui est bornée (mais non convergente). Il peut y avoir plusieurs conditions sur \(\sigma\) s’il y a plusieurs limites à calculer. La condition la plus forte définit le plan de convergence, où la transformée de Laplace converge.

Réponse impulsionnelle \(h_1\) :

\[H_1(s) = \frac{3}{s+2} - \frac{2}{s+1} \quad\text{si}\; \sigma>-2\]

La région de convergence correspond au plan complexe où la partie réelle de \(s\) est supérieure à \(-2\). \(H_1\) possède deux pôles (\(-1\) et \(-2\)) et un zéro (\(1\)). Les pôles sont à partie réelle négative : le système est donc stable.

Réponse impulsionnelle \(h_2\) :

\[H_2(s) = \frac{1}{2}\frac{1}{s+1-3j} + \frac{1}{2}\frac{1}{s+1+3j} \quad\text{si}\; \sigma>-1\]

La région de convergence correspond au plan complexe où la partie réelle de \(s\) est supérieure à \(-1\). \(H_2\) possède deux pôles (\(-1+3j\) et \(-1-3j\)) et un zéro (\(-1\)). Les pôles sont à partie réelle négative : le système est donc stable.

Exercice 9

Le calcul de la transformée en Z peut nécessiter de calculer la limite en \(n \to +\infty\) d’une fonction de \(z\). Cette limite est finie en imposant une certaine condition sur le module de \(z\). S’il y a plusieurs conditions pour obtenir une transformée en Z convergente, alors la condition la plus forte définit le plan de convergence, où la transformée en Z converge.

Réponse impulsionnelle \(h_1\) :

\[H_1(z) = \frac{7}{1-\frac{1}{3}z^{-1}} \quad\text{si}\; |z|>\frac{1}{3}\]

La région de convergence correspond au plan complexe où le module de \(z\) est supérieur à \(\frac{1}{3}\). \(H_1\) possède un zéro (\(0\)) et un pôle (\(1/3\)). Le pôle est dans le cercle unité : le système est donc stable.

Réponse impulsionnelle \(h_2\) :

\[\begin{split} H_2(z) &= \frac{1}{2j}\frac{1}{1-2e^{j\pi/4}z^{-1}} - \frac{1}{2j}\frac{1}{1-2e^{-j\pi/4}z^{-1}} \quad\text{si}\; |z|>2 \\ &= \frac{ 2\sin(\pi/4) z }{(z-2e^{j\pi/4})(z-2e^{-j\pi/4})} \quad\text{si}\; |z|>2 \end{split}\]

La région de convergence correspond au plan complexe où le module de \(z\) est supérieur à \(2\). \(H_2\) possède deux pôles (\(2e^{j\pi/4}\) et \(2e^{-j\pi/4}\)) et un zéro (\(0\)). Les pôles sont en dehors du cercle unité : le système est donc instable.

Exercice 10

Après avoir décomposé les fonctions de transfert en éléments simples, on peut utiliser les tables pour trouver les transformées de Laplace inverser, et donc :

\[ h_1(t) = (e^{-t}-e^{-2t})u(t), \qquad h_2(t) = \left( \cos(\sqrt{2}t) - \frac{3}{\sqrt{2}}\sin(\sqrt{2}t) \right) u(t). \]

Exercice 11

\[ h_1[n] = -2^n u[-n-1], \qquad h_2[n] = 2n2^n u[n]. \]

Exercice 12

Les deux filtres sont d’ordre 1. En les combinant, on obtient un filtre d’ordre 2 de fonction de transfert :

\[H(s) = H_1(s) \times H_2(s) = \frac{1}{a_1s+a_0}\frac{1}{b_1s+b_0}.\]

En ajoutant un troisième filtre d’odre 1, on obtient un filtre d’ordre 3.

Filtres numériques

Exercice 13

\[\begin{split} &H(z) = \frac{Y[z]}{X[z]} = \frac{1}{\frac{1}{2}-4z^{-1}} \\ \Leftrightarrow\qquad &Y[z] \left( \frac{1}{2}-4z^{-1} \right) = X[z] \\ \end{split}\]

Comme la transformée en Z est linéaire et que \(z^{-1}\) correspond à un retard, on aboutit à la relation temporelle suivante :

\[\begin{split} &\frac{1}{2}y[n] - 4y[n-1] = x[n] \\ \Leftrightarrow\qquad &y[n] = 2x[n] + 8y[n-1] \end{split}\]

Le signal \(y\) est donc la somme du signal \(x\) (avec un gain de 2) et du signal \(y\) (retardé d’un échantillon et avec un gain de 8) :

Exercice 14

Exercice 15

\[ H_1(s) = \frac{ 1 + 2z^{-1} z^{-2} }{ 1 + z^{-1} } \]

\[ H_2(z) = \frac{ 1 - \frac{7}{4}z^{-1} - \frac{1}{2}z^{-2} }{ 1 + \frac{1}{4}z^{-1} - \frac{1}{8}z^{-2} } \]

Exercice 16

Le filtre étant synthétisé avec la méthode des fenêtres, c’est un filtre RIF et il est donc forcément stable.

Les fenêtres envisageables sont les fenêtres de Hamming, Blackman et Kaiser.

La fenêtre de Kaiser, avec \(\beta=4,538\) par exemple, donnera l’ordre le plus faible. Sa largeur de transition est \(2,93/N\) et doit être égale à \(10/120\) : on obtient donc un ordre \(N=36\).

Filtres analogiques

Exercice 17

Ce filtre est un passe-bas. Il n’y a pas d’oscillation ni en bande passante ni en bande atténuée : c’est un filtre de Butterworth ou de Bessel. Sa fréquence de coupure est de 0,2 Hz.

Exercice 18

Ce filtre est un passe-bande. Il y a des oscillations en bande passante mais pas en bande atténuée : c’est un filtre de Tchebychev de type I. Ses fréquences de coupure sont 0,5 et 15 Hz.