Corrections

Modulation analogique

Exercice 1

Le signal modulé \(x\) a pour transformée de Fourier :

\[ X(f) = M(f) * \frac{1}{2j} \left[ \delta(f-f_p) - \delta(f+f_p) \right] \]

Au niveau du démodulateur, le signal modulé \(w\) a pour transformée de Fourier :

\[\begin{split} W(f) &= W(f) * \frac{1}{2} \left[ \delta(f-f_p) + \delta(f+f_p) \right] \\ &= M(f) * \frac{1}{4j} \left[ \delta(f-2f_p) - \delta(f) + \delta(f) - \delta(f+2f_p) \right] \\ &= \frac{1}{4j} \left[ M(f-2f_p) - M(f+2f_p) \right] \\ \end{split}\]

Le filtre passe-bas étant de fréquence de coupure \(f_c=f_p\), les deux termes \(M(f-2f_p)\) et \(M(f+2f_p)\) sont atténués. Finalement, le signal en sortie du filtre est nul.

Exercice 2

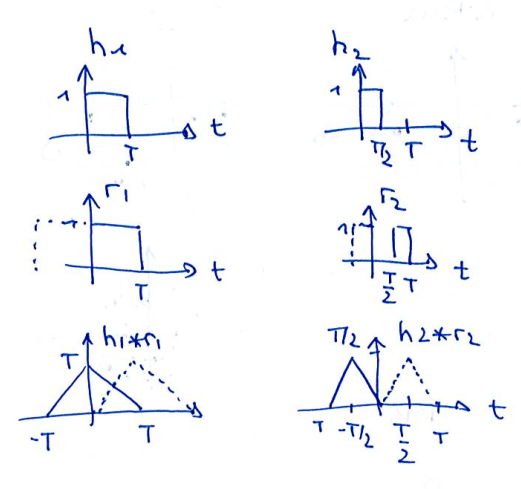
Le signal modulé est \(x(t) = m(t) \sin(2\pi f-p t)\) et le signal modulé est \(y(t) = m(t) \sin(2\pi f_q t)\). En conséquence, le spectre du signal modulé est :

\[ Y(f) = M(f) * \frac{1}{(2j)^2} \left[ \delta(f-f_p-f_q) - \delta(f-f_p+f_q) - \delta(f+f_p-f_q) + \delta(f+f_p+f_q) \right] \]

On remarque que lorsque \(f_q \neq f_p\) alors la démodulation ne fonctionne pas puisqu’on ne retrouve pas, dans les basses fréquences, le spectre original du signal \(m\).

Exercice 3

La technique de chiffrage du son consistait en deux étapes :

• modulation d’amplitude du signal à la fréquence \(f_\text{max}\) ;

• filtrage passe-bas avec une fréquence de coupure égale à \(f_\text{max}\).

Exercice 4

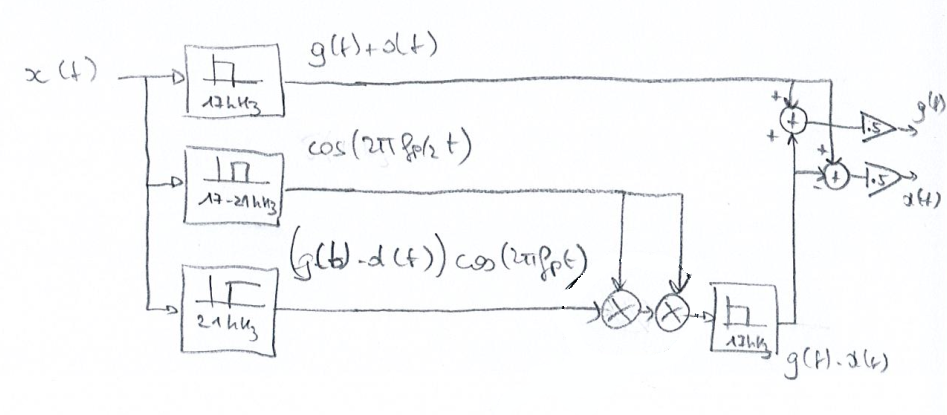
1. La présence d’un spectre représentant \(g(t)+d(t)\) permet d’avoir facilement accès à l’enregistrement en mono, avec une fréquence maximale de 15 kHz. Le spectre de \(g(t)-d(t)\) permet de fabriquer l’enregistrement stéréo. L’impulsion de Dirac en 19 kHz, qui correspond à la moité de 38 kHz, permet au récepteur de se caler sur cette fréquence de 38 kHz.

2. On peut écrire le signal \(x\) comme :

   \[ x(t) = x_1(t) + x_2(t) + x_3(t) \]

   où

   \[\begin{split} x_1(t) &= g(t)+d(t) \\ x_2(t) &= \cos(2\pi f_p/2 t) \\ x_3t() &= (g(t)-d(t)) \cos(2\pi f_p t) \end{split}\]

   où \(f_p=38\) kHz.

Modulation numérique

Exercice 5

Vérifiez avec cet outil de simulation.

Exercice 6

Fig. 46 Exemple de modulation OOK.

Fig. 47 Exemple de modulation 4-ASK : les symboles sont alignés sur une droite passant par l’origine.

Fig. 48 Exemple de modulation 2-PSK : les symboles sont situés sur un cercle centré sur l’origine.

Fig. 49 Exemple de modulation 8-QAM.

Exercice 7