Conclusion#

Mathematical morphology gathers operators that work on the form of objects. We have studied some operators applied to binary images, but there are extensions of these techniques to grayscale images.

The results given by the four main operators on binary images are listed in the following table.

../_images/greece1.png

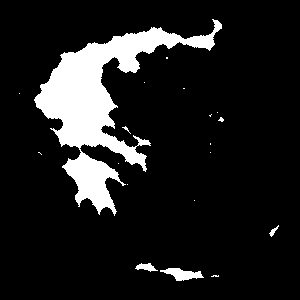
Original image
../_images/greece-dilation.png

Dilation \(\oplus\)

  • increases the size of objects (e.g. the islands are bigger)

  • fills the small holes (e.g. the Gulf of Corinth does not more exist after dilation)

  • welds close objects (e.g. some islands are grouped into a larger island)
../_images/greece-erosion.png

Erosion \(\ominus\)

  • decreases the size of objects (e.g. Crete is smaller)

  • widens the holes (e.g. the Gulf of Corinth is bigger)

  • separates the connected objects by a small bridge (e.g. the Peloponnese and mainland Greece are now disconnected)

  • removes small items (e.g. small islands have disappeared)
../_images/greece-opening.png

Opening \(\circ\)

  • conserve the size of the objects (while they can be slightly distorted)

  • removes small objects (e.g. small islands have disappeared)

  • smoothes the contours (e.g. the coasts are no more jagged)
../_images/greece-closing.png

Closing \(\bullet\)

  • conserve the size of the objects (while they can be slightly distorted)

  • fills small holes (e.g. gulfs and lakes are removed)

  • welds close shapes (e.g. some separated islands now form only one)