Deconvolution#

The objectives of this exercise are:

  • know how to apply a specific degradation to an image

  • understand why naive deconvolution does not work

  • implement a Wiener filter

Original and noisy images#

../_images/27c9fbfaa060a4e8f2bb7d58ae5d8e8b97ad2a4ee0e7d637bed0dc953b476080.png

The “USAF 1951” resolution chart is a tool for measuring the resolution of optical instruments. It was designed by the U.S. Air Force. Its interest in image processing is to measure the resolution capacity of methods. Here, it is interesting because once blurred, it is difficult to count the lines and read the figures.

Inverse filter on the non-noisy image#

../_images/b1d96140f701b827777b0fe56ce0d3e512d236a6370fb875807a6a12d4bfe626.png

In the absence of noise, the inverse filter works perfectly (except for a translation, due to the PSF size).

Inverse filter with noise#

# Calcul de la variance d'un bruit blanc gaussien pour un RSB donné
def variance(snr, x):
    M, N = x.shape
    return norm(x)**2 / (M*N) * 10**(-snr/10)
../_images/0e8e8efb132757973283df0cdd019c31cd6a80cb4632d55eea9b846b8824ef5a.png

On the contrary, when the image is noisy (even slightly: here SNR equals 40 dB), the restoration is not at all acceptable!

Wiener filter with noise#

Be careful, there is another wiener function (skimage.filters.wiener), but it is more tricky. Instead, use skimage.restoration.wiener, not forgetting to add clip=False.

../_images/0f99ddcd32974702fadc1332ec025cc9571364e777c1a55e460dbee6a88e033a.png ../_images/e6e095d96eb5cf39602e8eb76affef95d7d0a8e4de566ce9dd3e081da5e1c4ad.png

These first results have been obtained for three values of \(\lambda\). They show that in terms of MSE, there is a compromise to be made between denoising and deconvolution. If \(\lambda\) is too low, the restored image is deconvolved but remains very noisy; if \(\lambda\) is too large then the image remains blurry.

For a better analysis, we represent the MSE with respect to \(\lambda\).

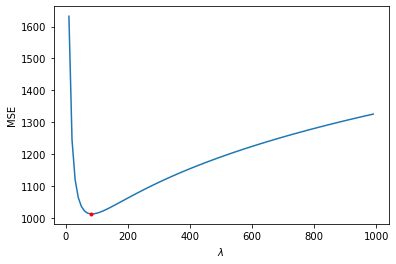
../_images/642db5b974ab8d96091e5ad9d265e9294eaa9442144a6ab6efe980e03dcf3c1b.png 
The best restoration is obtained for lambda = 80 and gives MSE = 1327.96.
../_images/c09592f9daaf502e61c899da63bdfee4d184591fe782a85b4e07113b693b27ba.png

I find personally that this value of \(\lambda\) gives a less clear picture than for lower values of \(\lambda\) (as presented above). This shows that the MSE does not perfectly represent the perceived quality. But the perceived quality is subjective and depend on the desired objective, whereas MSE is an objective measure.

Finally, as for denoising methods, it is very difficult to set a priori the value of the parameter \(\lambda\).