Interpolation#

First, make rotations of angle 90° with a 0-order (nearest neighbour) interpolation.

Rotation with rotations of angle 90° and 0-order interpolation, MSE = 0.000:
../_images/15dd252423595ba6f2afdbeba0d7e5f14e9f8cbd9ca18da293e394eb8715597e.png

In this configuration, the mean square error (MSE) is zero, meaning that the interpolations made along the sequence of rotation are perfect, i.e. the image is not changed.

Now, make rotations of angle 40°, with different interpolations (nearest neigbour, bilinear and bicubic).

Rotation with rotations of angle 40° and 0-order interpolation, MSE = 0.325:
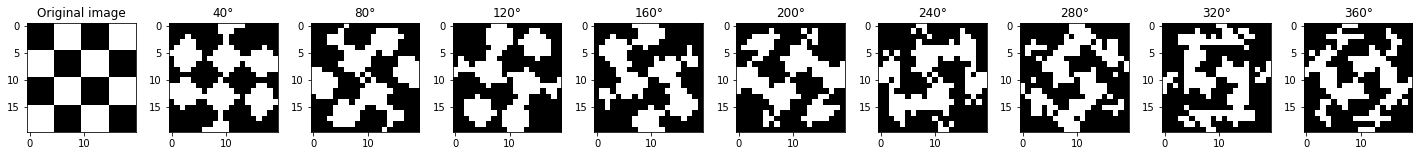
../_images/72d21c8342618e1ed46a9b1c0393df157ef51edc0311d9ad7fbc97f42ce4e0ef.png 
Rotation with rotations of angle 40° and 1-order interpolation, MSE = 0.184:
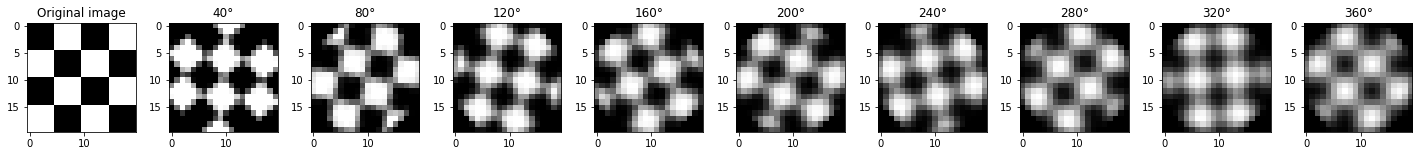
../_images/b71162d0ed13ac755f410d4f4c4daa18f20493432a4eb60bb9448682caf7a134.png 
Rotation with rotations of angle 40° and 3-order interpolation, MSE = 0.137:
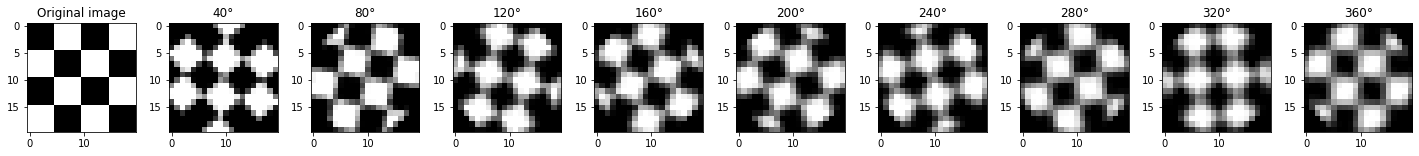
../_images/309e551a568a6896d17c1cab5cd37db306d6661492393f1759b39566d5ef38ba.png

In this example, a visual inspection of the result (last image) clearly shows that the nearest-neigbour interpolation is not satisfactory. This is confirmed by the MSE which is not the best MSE among the different results given by the interpolations.

In this example, the best interpolation is given by the bicubic interpolation.

Try to compare the results for different step angles, and different images!