Corner detection

To detect the corners of objects in an image, one can start by detecting edges then determining where two edges meet. There are however other methods, among which:

• the Moravec detector [Moravec 1980],

• the Harris detector [Harris & Stephens 1988].

Moravec detector

The principle of this detector is to observe if a sub-image, moved around one pixel in all directions, changes significantly. If this is the case, then the considered pixel is a corner.

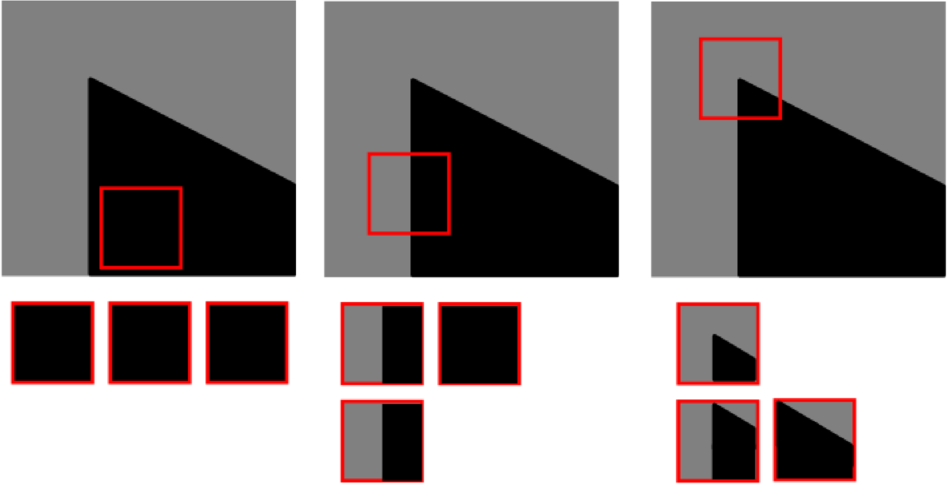
Fig. 121 Principle of Moravec detector. From left to right : on a flat area, small shifts in the sub-image (in red) do not cause any change; on a contour, we observe changes in only one direction; around a corner there are significant changes in all directions.

Mathematically, the change is characterized in each pixel \((m,n)\) of the image by \(E_{m,n}(x,y)\) which represents the difference between the sub-images for an offset \((x,y)\):

\[ \forall m,n,x,y \qquad E_{m,n}(x,y) = \sum_{u,v} w_{m,n}(u,v) \big[f(u+x,v+y)-f(u,v)\big]^2 \]

where:

• \(x\) and \(y\) represent the offsets in the four directions: \((x,y) \in \{(1,0),\,(1,1),\,(0,1),\,(-1,1)\}\),

• \(w_{m,n}\) is a rectangular window around pixel \((m,n)\),

• \(f(u+x,v+y)-f(u,v)\) is the difference between the sub-image \(f(u,v)\) and the offset patch \(f(u+x,v+y)\),

In each pixel \((m,n)\), the minimum of \(E_{m,n}(x,y)\) in the four directions is kept and denoted \(F_{m,n}\). Finally, the detected corners correspond to the local maxima of \(F_{m,n}\), that is, at pixels \((m,n)\) where the smallest value of \(E_{m,n}(x,y)\) is large.

It turns out that Moravec detector has several limitations. First, \(w\) is a binary window and therefore the detector considers all pixels in the window with the same weight. When the noise in the image is high, it can lead to false corner detections. Second, only four directions are considered. Third, the detector remains very sensitive to edges because only the minimum of \(E\) is considered. For these reasons, Harris has proposed a detector to overcome these limitations.

Harris detector

To avoid a noisy response, the rectangular window \(w\) of the Moravec detector is replaced by a Gaussian window \(w\) in the expression of \(E_{m,n}(x,y)\).

To extend the Moravec detector to all directions, not limited to the initial four directions, a Taylor series expansion is performed on the shifted sub-image \(f(u+x,v+y)\):

\[ f(u+x,v+y) \approx f(u,v) + x \,\partial_x f(u,v) + y \,\partial_y f(u,v). \]

Therefore :

\[ E_{m,n}(x,y) \approx \sum_{u,v} w_{m,n}(u,v) \big[ x \,\partial_x f(u,v) + y \,\partial_y f(u,v) \big]^2 \]

This expression can be written in the following matrix form:

\[\begin{split} E_{m,n}(x,y) \approx \begin{pmatrix} x & y \end{pmatrix} M \begin{pmatrix} x \\ y \end{pmatrix} \end{split}\]

where

\[\begin{split} M = \sum_{u,v} w_{m,n}(u,v) \begin{pmatrix} (\partial_x f)^2 & \partial_x f \,\partial_y f \\ \partial_x f \,\partial_y f & (\partial_y f)^2 \\ \end{pmatrix} \end{split}\]

Finally, the last limit of the Moravec detector can be avoided by considering a new measure of the presence of a corner: more information about the intensity change in the window can be obtained by analyzing the eigenvalues \(\lambda_1\) and \(\lambda_2\) of the matrix \(M\) (Fig. 122). Indeed, the presence of a corner is attested if the derivatives of \(f\) are very large, then \(M\) has large coefficients, and its eigenvalues are also very large.

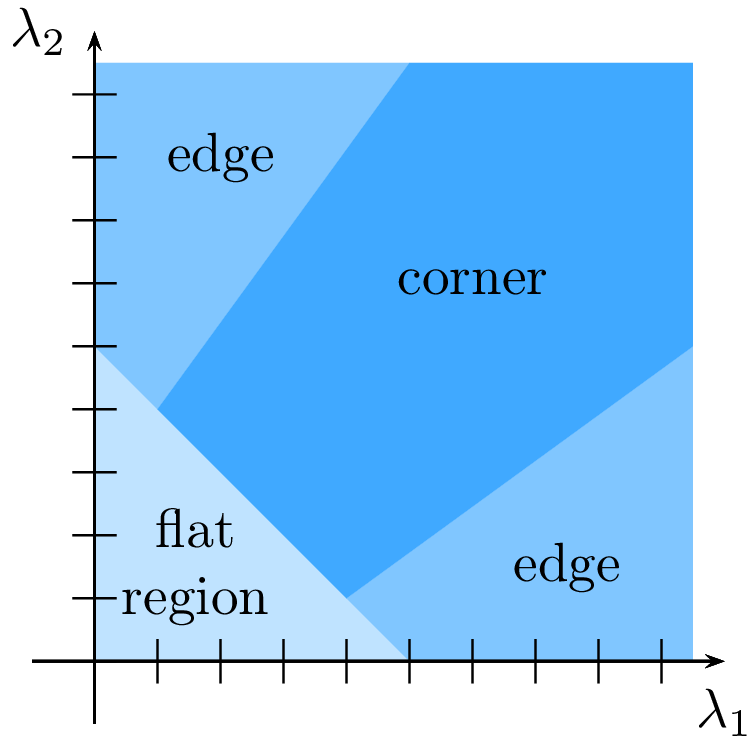
Fig. 122 Decision to be taken in function of the eigenvalues.

The calculation of the eigenvalues of \(M\) can be difficult, so an alternative is to calculate:

\[ R = \mathrm{det}(M) - k (\mathrm{trace}(M))^2 = \lambda_1 \lambda_2 - k(\lambda_1 + \lambda_2)^2 \]

with \(0.04 < k < 0.06\).

Thus, the values of \(R\) are low in a flat region, negative on an edge, and positive on a corner (Fig. 123).

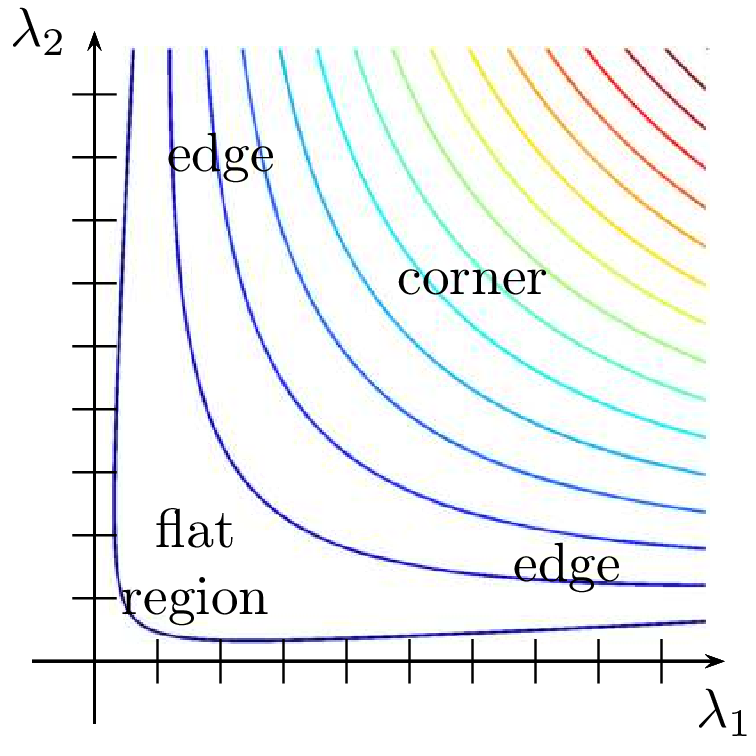
Fig. 123 Decision to be taken in function of \(R\).

The Harris detector is illustrated on the example of Fig. 124.

Fig. 124 Harris detector. The binary images represent the negative (contours), weak (flat areas) and positive (corners) values of the coefficient \(R\).