Transformée de Fourier discrète d’un signal numérique#
Le signal temporel est une porte :
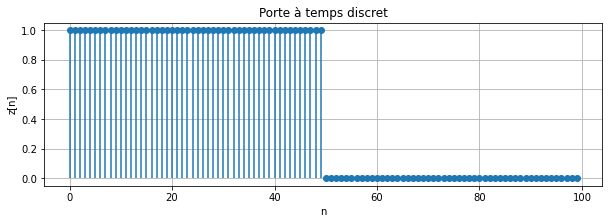
Attention ! Le signal contient 100 échantillons (de 0 à 99) et l’échantillon en \(n=50\) est nul !
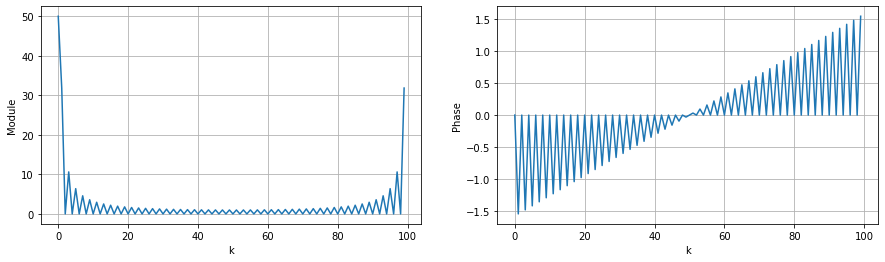
Spectre non centré, en fonction des échantillons#
Par simplicité et lisibilité, les spectres sont tracés avec plot mais ils restent discrets !
Z1 = fft.fft(z)
k1 = np.arange(N)
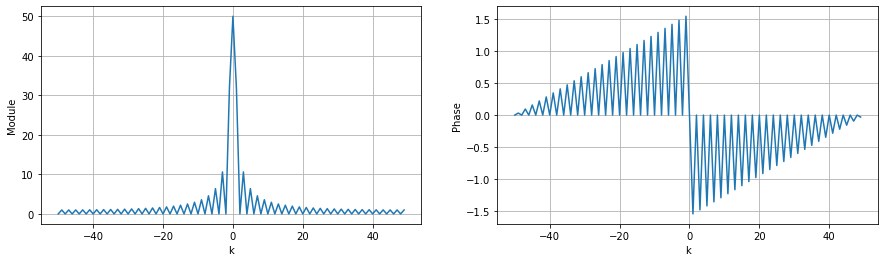
Spectre centré, en fonction des échantillons#
k2 = k1 - np.floor(N/2)
Z2 = fft.fftshift(Z1)
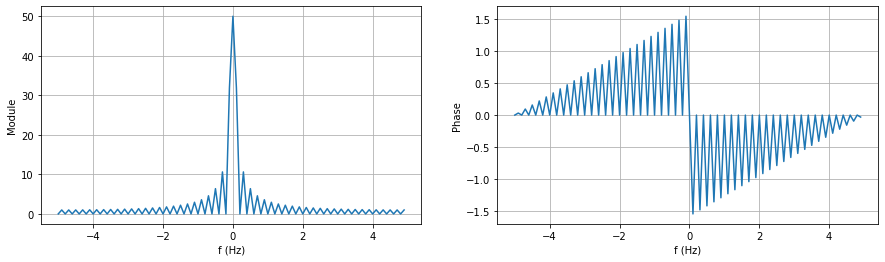
Spectre centré, en fonction de la fréquence#
On vérifie que les abscisses représentent bien une période du spectre (entre \(-f_e/2\) et \(f_e/2\)).
f = k2/(N*Te)
Application#
Le signal temporel est :
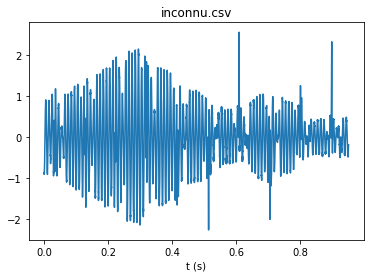
Son spectre est :
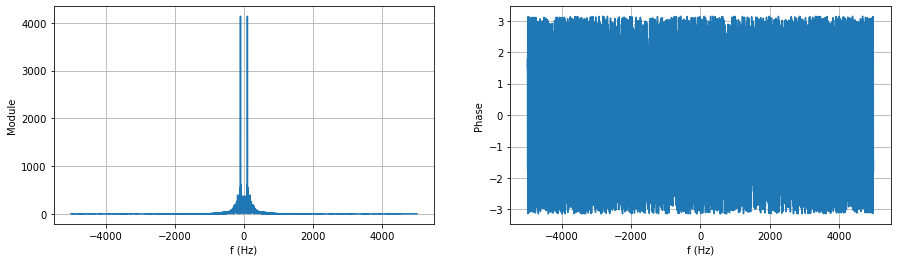
La fonction matplotlib.pyplot.xlim permet de zoomer sur la partie intéressante :
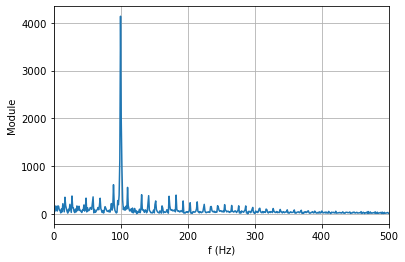
La fréquence principale du signal est donc à 100 Hz.