Signaux élémentaires

Contenu

Signaux élémentaires#

Différents signaux seront régulièrement utilisés dans le cours : ils sont définis ici. La plupart peuvent être définis à temps continu ou à temps discret.

Sinusoïde#

En temps continu, la sinusoïde a pour expression :

\[ x(t) = A \sin(2 \pi f t + \varphi) \]

dont les paramètres sont :

\(A\) est l”amplitude,
\(f\) est la fréquence,
\(\varphi\) est la phase. Remarquez que si \(\varphi=0\), alors \(x(t)\) est un sinus, et si \(\varphi=\pi/2\), alors \(x(t)\) est un cosinus.

La sinusoïde en temps continu est périodique de période \(1/f\) ou, de manière équivalente, de fréquence \(f\).

En temps discret, la sinusoïde a la même expression :

\[ x[n] = A \sin(2 \pi f n + \varphi) \]

Le sinus est créé en Python avec la fonction numpy.sin.

Exponentielle complexe#

En temps continu, l’exponentielle complexe a pour expression :

\[ x(t) = \exp(j 2 \pi f t + \varphi) = \cos(2 \pi f t + \varphi) + j \sin(2 \pi f t + \varphi) \]

En temps discret, c’est la même expression (en remplaçant les parenthèses dans \(x(t)\) par des crochets). L’exponentielle est créée en Python avec la fonction numpy.exp, et le nombre complexe \(j\) est obtenu avec 1j.

À cause du nombre complexe \(j\), le signal est à valeurs complexes. Pour le représenter, il faut être dans un espace à trois dimensions (la variable, la partie réelle et la partie imaginaire). De cette manière, l’exponentielle complexe ressemble à une queue de cochon, ou un tire-bouchon. Remarquez que la variable \(f\), souvent appelée fréquence, peut tout à fait être négative : dans ce cas, l’exponentielle complexe tourne dans le sens inverse.

Sinus cardinal#

Le sinus cardinal, noté \(\mathrm{sinc}\), a pour définition :

\[\begin{split} \mathrm{sinc}(t) = \begin{cases} \displaystyle \frac{\sin(\pi t)}{\pi t} &\text{si}\quad t \neq 0 \\ 1 &\text{si}\quad t = 0 \end{cases} \end{split}\]

Un sinus cardinal ressemble à un cosinus donc l’amplitude décroît lorsqu’on s’éloigne de \(t=0\).

Encore une fois, le sinus cardinal à temps discret a la même expression (avec des crochets à la place des parenthèses). Le sinus cardinal est obtenu en Python avec la fonction numpy.sinc.

Échelon#

L’échelon (également appelé fonction de Heaviside) a pour définition :

\[\begin{split} u(t) = \begin{cases} 0 &\text{si}\quad t < 0 \\ 1 &\text{si}\quad t \geq 0 \end{cases} \end{split}\]

L’échelon est donc nul pour \(t<0\) et égal à 1 sinon. Il existe aussi une version à temps discret.

Il n’existe pas de fonction permettant de générer un échelon en Python : il faut passer par des instructions spécifiques, comme par exemple dans le code suivant :

# Modules à importer
import numpy as np
import matplotlib.pyplot as plt

# Tout d'abord, générer la liste des instants d'échantillonnage
# Par exemple ici : 11 échantillons répartis entre -5 et 4
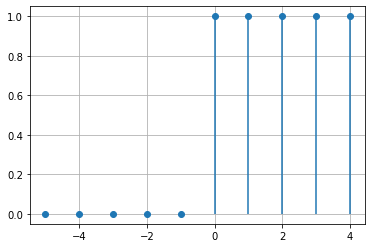
n = np.arange(-5, 5)

# L'échelon est obtenu avec la fonction numpy.where
# qui affecte la valeur 1 ou 0 suivant la condition
u = np.where(n>=0, 1, 0)

# Affichage
plt.stem(n, u, basefmt=" ")
plt.grid()
plt.show()

../_images/edfeba9a1291dc06023e9873bc4298e40907bd862dff5bb91e5c9a8d4626450d.png

Porte#

La porte (ou fonction rectangle) a pour définition :

\[\begin{split} \mathrm{rect}(t) = \begin{cases} 0 &\text{si}\quad |t| > \frac{1}{2} \\ 1 &\text{si}\quad |t| \leq \frac{1}{2} \end{cases} \end{split}\]

Cette porte est de longueur 1 et centrée sur 0.

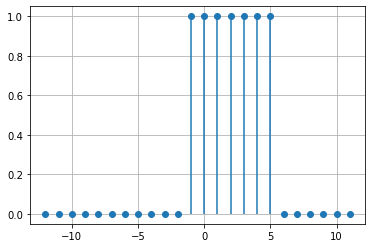
Comme pour l’échelon, la porte peut être définie en Python avec la fonction numpy.where. Par exemple, l’illustration ci-dessous est une porte discrète centrée sur 2 et de longueur 7 :

# Porte définie entre -5 et 10,
# représentée entre -12 et 12
n = np.arange(-12, 12)
r = np.where( (n>=-1) & (n<=5) , 1, 0)
plt.stem(n, r, basefmt=" ")
plt.grid()
plt.show()

../_images/c0b2d23958450e694456861e513be69ac34aa3bc941f7e2ebecdfcd0ceed478e.png

Impulsion de Dirac#

L’impulsion de Dirac est telle que :

\[ \delta(t) = 0 \;\text{si}\; t \neq 0 \qquad\text{et}\qquad \int \delta(t) dt = 1 \]

L’impulsion de Dirac n’est pas une fonction, au sens mathématique, car \(\delta(0)\) n’est pas défini : c’est en fait une distribution. Pour cette raison, on représente ce signal par une flèche, qui signifie que la valeur n’est pas définie en 0.

C’est un signal non représentable physiquement car il n’existe pas dans la nature. Mais c’est une conceptualisation mathématique bien pratique. Un exemple réaliste qui s’en approcherait serait le son produit lorsqu’on tape d’un coup bref dans ses mains. On peut l’approcher par une porte dont la largeur tend vers 0 et l’amplitude vers l’infini.

L’impulsion de Dirac a des propriétés particulières, notamment :

\(f(t) \delta(t) = f(0) \delta(t)\)
\(f(t) \delta(t-\tau) = f(\tau) \delta(t-\tau)\)

De la dernière propriété découle la suivante :

\[ \int f(t) \delta(t-\tau) dt = \int f(\tau) \delta(t-\tau) dt = f(\tau) \int \delta(t-\tau) dt = f(\tau). \]

À l’inverse des signaux précédents, l’impulsion de Dirac ne peut pas s’écrire en temps discret. Il existe cependant un signal qui s’en approche : l”impulsion discrète.

Impulsion discrète#

L’impulsion discrète est l’équivalent à temps discret de l’impulsion de Dirac. C’est une fonction mathématique classique car elle est définie en tout point :

\[\begin{split} \delta[n] = \begin{cases} 0 \;\text{si}\; n \neq 0 \\ 1 \;\text{si}\; n = 0 \end{cases} \end{split}\]

L’impulsion discrète est également appelée impulsion de Kronecker.

La fonction numpy.where peut encore être utilisée pour définir une impulsion discrète en Python :

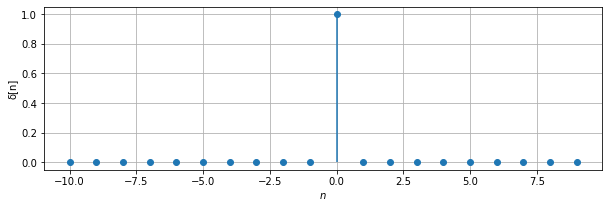
n = np.arange(-10, 10)
d = np.where(n==0, 1, 0)

plt.figure(figsize=(10,3))
plt.stem(n, d, basefmt=" ")
plt.xlabel("$n$")
plt.ylabel("δ[n]")
plt.grid()
plt.show()

../_images/d812ed05e4ebe461030c238a8c65a639ecb183edd134fb676fa759e4b1b0b14e.png

Peigne de Dirac#

Le peigne de Dirac est défini par (\(T > 0\)) :

\[ Ш_T(t) = \sum_{k=-\infty}^{+\infty} \delta(t-kT) \]

Le peigne de Dirac est également appelé train d’impulsion, fonction d’échantillonnage ou distribution Cha (en raison de sa ressemblance avec la lettre cyrillique Ш).

2