Représentation de signaux

Par convention, les importations de modules sont faites en début de notebook.

import numpy as np                    # Calcul et fonctions scientifiques
import matplotlib.pyplot as plt       # Affichage

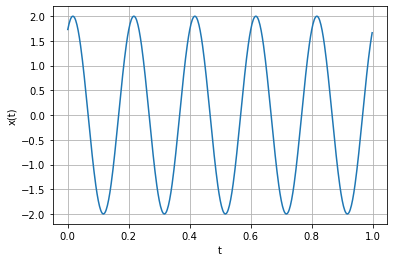
Signal sinusoïdal

On modifie le code de l’énoncé…

# Vecteur des abscisses : un point tous les 2 ms entre 0 et 1 s
t = np.arange(0, 1, 2e-3)

# Paramètres
A = 2
f = 5
phi = np.pi/3

# Sinusoïde
x = A * np.sin(2*np.pi*f*t + phi)

print("Signal de dimensions : ")
print(x.shape)

# Affichage
plt.plot(t, x)
plt.xlabel("t")
plt.ylabel("x(t)")
plt.grid()
plt.show()

Signal de dimensions : 
(500,)

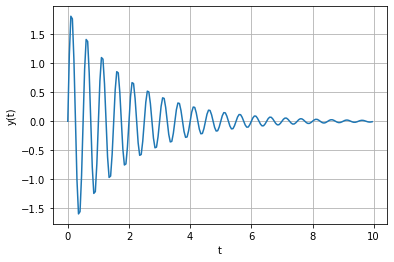
Sinusoïde amortie

De nouveau, on s’inspire du code précédent…

L’exponentielle (numpy.exp) et le sinus sont calculés en deux instructions pour plus de clarté.

# Vecteur des abscisses : un point tous les 0,05 s entre 0 et 10 s
t = np.arange(0, 10, .05)

# Paramètres
A = 2
a = 0.5
f = 2

# Sinusoïde amortie
expo = np.exp(-a*t)
sinus = np.sin(2*np.pi*f*t)
y = A * expo * sinus

# Affichage
plt.plot(t,y)
plt.xlabel("t")
plt.ylabel("y(t)")
plt.grid()
plt.show()

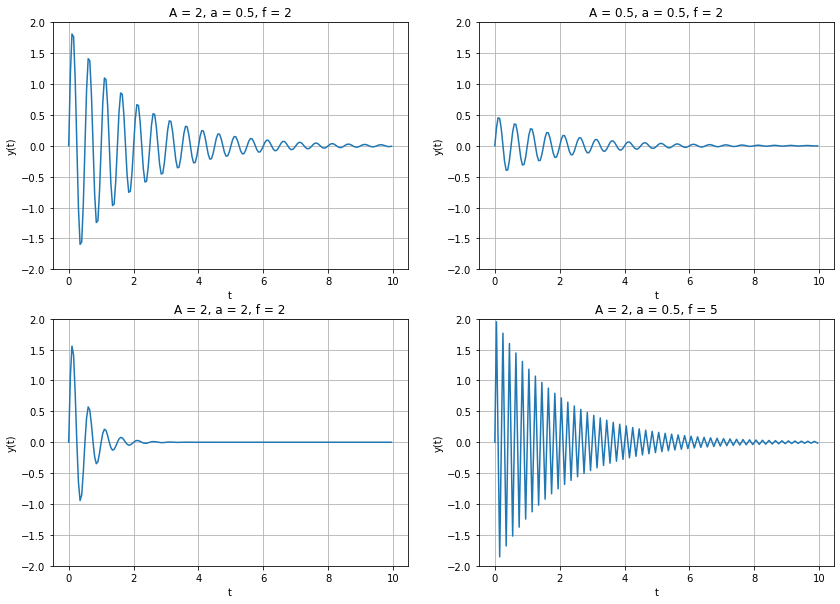
Quelle est l’influence des paramètres ?

Porte

N’oubliez pas : une porte ou une impulsion peuvent être définies avec numpy.where.

On veut tracer :

\[\begin{split} \begin{align*} z[n] &= A\,\mathrm{rect}\left(\frac{n-m}{N}\right) \\ &= \begin{cases} A &\text{si}\quad \left|\frac{n-m}{N}\right| \leq \frac{1}{2} \\ 0 &\text{si}\quad \left|\frac{n-m}{N}\right| > \frac{1}{2} \end{cases} \\ &= \begin{cases} A &\text{si}\quad m-\frac{N}{2} \leq n \leq m+\frac{N}{2} \\ 0 &\text{sinon} \end{cases} \end{align*} \end{split}\]

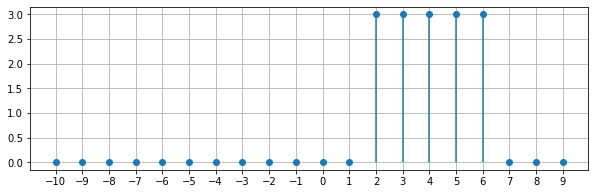
Donc avec \(A=3\), \(m=4\) et \(N=5\), le signal \(z\) est égal à \(3\) entre \(1,5\) et \(6,5\) et nul ailleurs.

On peut donc définir une porte entre \(2\) et \(6\) ou, si on est plus malin et fainéant, recopier la définition du signal porte en redéfinissant le vecteur des abscisses : c’est ce que je fais ci-dessous.

# paramètres
A, m, N = 3, 4, 5

# Abscisses
n = np.arange(-10, 10)

# Signal
n2 = (n-m) / N
z = 3 * np.where( (n2>=-.5) & (n2<=.5) , 1, 0)

# Affichage
plt.figure(figsize=(10,3))
plt.stem(n, z, basefmt=" ")
plt.xticks(n)
plt.grid()
plt.show()

Concentration de CO₂

Chargement des données avec la fonction numpy.loadtxt, en précisant que la première ligne est à éviter, et que les données sont délimitées par une virgule.

X = np.loadtxt("world-co2.csv", skiprows=1, delimiter=",")
print(X.shape)

(1875, 2)

Il y a 1875 enregistrements sur deux colonnes, lesquelles correspondent aux années et à la concentration en CO₂ atmosphérique, à l’échelle mondiale, mesurée en parties par million (ppm) (Source : Our World in Data, Atmospheric concentrations of CO2 continue to rise).

On peut donc représenter sur différentes échelles de temps l’évolution de ce gaz à effet de serre.