Produit de convolution

Produit de convolution#

Avant propos#

Le produit de convolution entre deux signaux \(x\) et \(y\) à temps discret est défini par :

\[ (x*y)[n] = \sum_{m=-\infty}^{+\infty} x[m]y[n-m]. \]

La fonction numpy.convolve calcule le produit de convolution et renvoie le résultat complet (full) ou tronqué (same et valid).

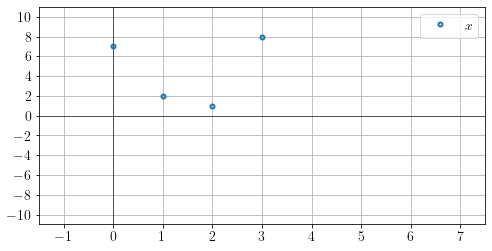
x	= [ 7, 2, 1, 8 ]   (len = 4)
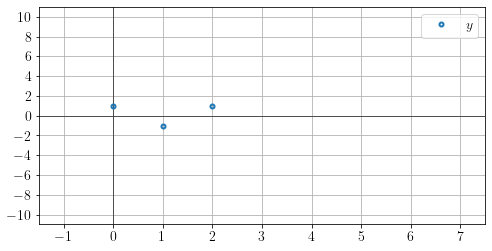
y	= [ 1, -1, 1 ]   (len = 3)
"full"	= [ 7, -5, 6, 9, -7, 8 ]   (len = 6)
"same"	= [ -5, 6, 9, -7 ]   (len = 4)
"valid"	= [ 6, 9 ]   (len = 2)
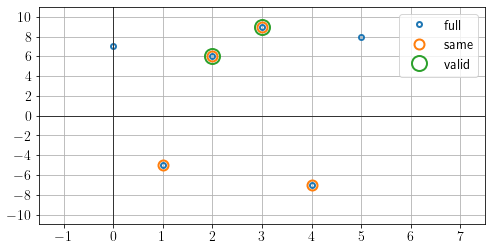
../_images/4d56839e69bf149f75eda2e8c11b18d239419f81bf0251d8806207a3a4ac694c.png ../_images/2682781d582ce5c50e268de2859ccc4921d0b1614afb7d7df6c222f72b9f55e9.png ../_images/d2cd441c9e5cb86facfb67b6efcf9beac68b3115803deb3d8af6afcb8b08d52c.png

Premier produit de convolution#

Comme pour la porte, l’impulsion discrète est définie avec numpy.where.

Attention à l’utilisation de la fonction numpy.arange utilisée pour définir les abscisses !

n = np.arange(-10, 10+1)

x = np.sin(2*np.pi*n/10)
y = np.where( n==5 , 3, 0)

z = np.convolve(x, y, mode="same")
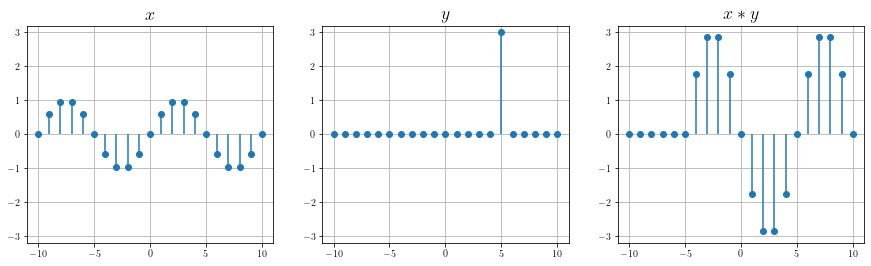
../_images/aff3d1f14aaf85269628b78951ed7b6e95899d2cf93e18edac23b17c64c57d59.png

  • On voit là l’effet de la convolution par une impulsion discrète : le signal \(x\) est décalé de 5 échantillons (lieu de l’impulsion) et amplifié de 3 (amplitude de l’impulsion).

  • Mais comment expliquer la présence d’échantillons nuls en début du signal \(x*y\) ?

Deuxième produit de convolution#

n = np.arange(-10, 10+1)

x = np.where( np.absolute(n)==1 , 1, 0) + np.where( n==0 , 2, 0)
y = np.where( n==-1 , -1, 0) + np.where( n==1 , 1, 0)

z = np.convolve(x, y, mode="same")
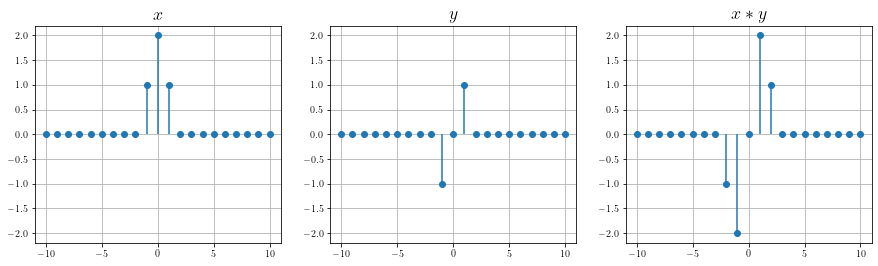
../_images/9642b80e7b8c4fccfde27dd4c2ab11472973387d173c03d9b39a8a4dd5c7c09a.png

Détail du calcul du produit de convolution :

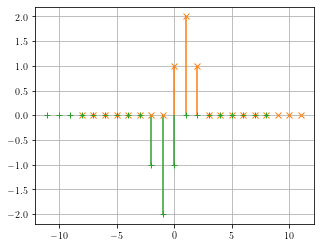
../_images/f62f60435e1f09b8790d7723283634efea3cc21eadc7527f017170d44c235242.png

  • Comme précédemment, la convolution par chaque impulsion de \(y\) va décaler et amplifer le signal \(x\) d’autant. La convolution de la somme étant la somme des convolutions (opération linéaire), alors le résultat \(x*y\) est la somme des deux convolutions.

Troisième produit de convolution#

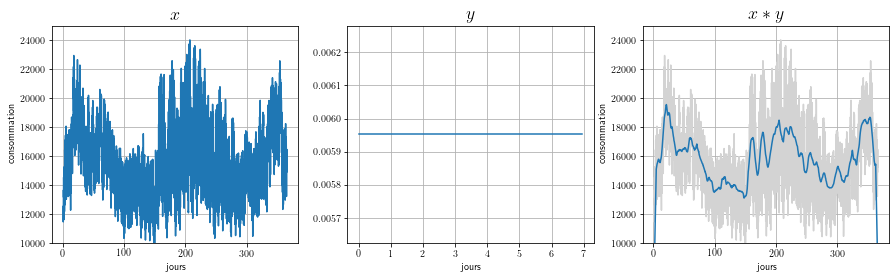
../_images/42a6ca5c7794a8e4805847974bfeac6c58954a7578f004d8891d0cfdbfc49627.png

  • La convolution par un porte revient à calculer chaque échantillon de \(x*y\) comme la moyenne de 24×7 échantillons de \(y\).

  • On procède donc à un moyennage du signal, qui a pour effet d’adoucir (lisser) le signal très perturbé (« bruité ») par une porte. C’est une véritable technique pour débruiter un signal.

Contenu