Exercices sur feuille#
Exercice 1#
Montrez que l’autocorrélation d’un signal périodique est également périodique et de même période.
Exercice 2#
Démontrez que le maximum de l’autocorrélation est en 0.
Exercice 3#
Calculez l’autocorrélation du signal ci-dessous, puis représentez-la pour \(N=2\).
\[\begin{split}
x[n] =
\begin{cases}
1 \quad&\text{si } -N \leq n \leq N \\
0 \quad&\text{sinon} \\
\end{cases}
\quad\text{où}\, N\in\mathbb{N}.
\end{split}\]
Exercice 4#
Un signal audio \(s(t)\) est émis par un haut-parleur et un microphone enregistre le signal reçu \(x(t)\). Ce signal \(x(t)\) est la somme du son provenant directement du haut-parleur ainsi que du son réfléchi par un mur :
\[
x(t) = s(t) + a\,s(t-d)
\]
où \(a\) est l’atténuation et \(d\) le retard dus à la réflexion sur le mur.
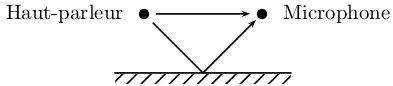
Déterminez l’autocorrélation de \(x(t)\) en fonction de l’autocorrélation de \(s(t)\).
Comment peut-on obtenir \(a\) et \(d\) à partir de l’autocorrélation ?