Produit de convolution#
Définition#
Le produit de convolution est une opération mathématique entre deux signaux qui calcule un troisième signal. Il est noté \(*\). Il décrit l’effet que produit un instrument de mesure ou un système sur une mesure, caractérisé par sa réponse impulsionnelle \(h\).
Fig. 2 Illustration du produit de convolution.#
Le produit de convolution entre deux signaux \(x\) et \(h\) produit un troisième signal \(y\).
Exemples#
L’animation ci-dessous illustre l’effet du produit de convolution entre les signaux \(x\) et \(h\). La première opération effectuée lors du calcul d’une convolution est le renversement et le décalage temporel d’un des deux signaux (ici nous avons choisi de renverser \(h(t)\)). La valeur du décalage \(t\) est modifiable à l’aide de la souris (ou du doigt). Ensuite, les signaux \(x(\tau)\) et \(h(t-\tau)\) sont multipliés entre eux et l’aire obtenue (représentée par la surface verte sur le quatrième graphe) correspond à \(y(t)\). En faisant glisser \(t\), on obtient le signal \(y(t)\) en entier.
Dans cette deuxième animation (ci-dessous), vous pouvez dessiner les signaux à temps discret \(x\) et \(h\) pour visualiser le résultat sur \(y\).
Exemple
La figure 3 représente les signaux \(x\), \(h\) et \(y\) dans le cas d’une simulation réaliste : le système de suspension d’un véhicule. Si \(x\) représente le profil de la route (ici, avec deux bosses) et que \(h\) est le signal qui caractérise le système de suspension, alors le véhicule va osciller suivant le signal \(y\).
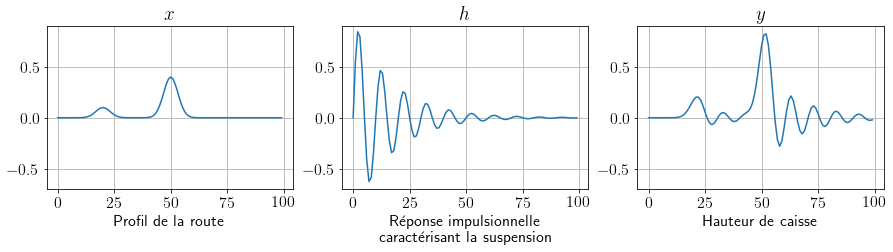
Fig. 3 Simulation d’une suspension (désagréable) de véhicule.#
Dans ce cas, les passagers vont être pas mal secoués, un peu comme dans une 2CV…
Exemple
En physique, un spectre représente la quantité de lumière émise ou transmise par un objet. Il est mesuré par un spectromètre. Or, un spectromètre n’est jamais parfait, comme tous les instruments de mesure. Malgré la qualité de sa conception, il reste toujours un peu de « flou ». Ce principe est représent Fig. 4 : \(x\) est le spectre réel de l’objet, tel qu’on voudrait le voir, mais à cause du flou introduit par le spectromètre (signal \(h\)), l’observation n’est pas aussi précise (signal \(y\)). En particulier sur cet exemple, la première raie, très petite, n’est plus visible.
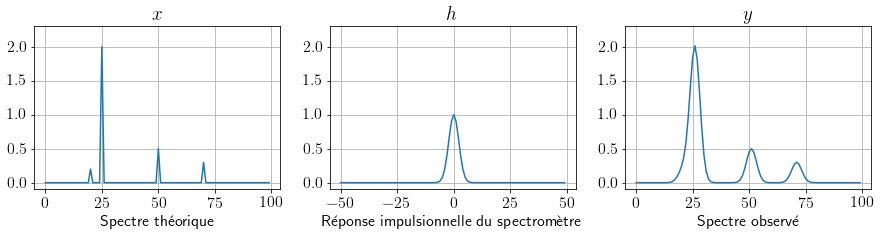
Fig. 4 Simulation d’un spectre de lumière observé avec un spectromètre.#
Exemple
Le produit de convolution, modélise également l’effet du filtrage d’un signal, comme on le verra en deuxième année. Dans l’exemple représenté Fig. 5, un effet sonore est appliqué sur le signal audio \(x\) par l’intermédiaire du filtre \(h\) (qui est appelé passe-bas), et cela résulte en le signal \(y\).
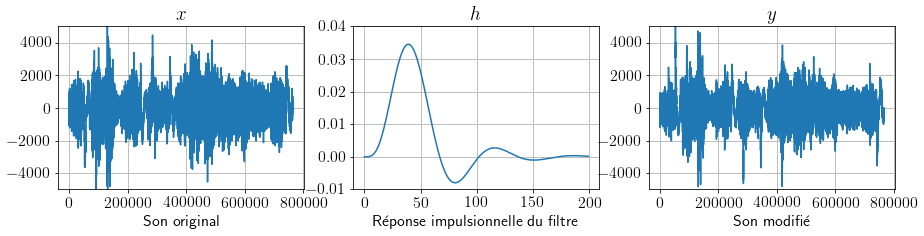
Fig. 5 Application d’un effet sonore.#
Vous pouvez constater l’effet du filtrage en écoutant le signal audio original :
… et le signal filtré :
Propriétés#
Soient \(f\), \(g\) et \(h\) des signaux (à temps continu ou discret), et \(a\) une constante. Le produit de convolution vérifie les propriétés suivantes.
En définissant \(x_{t_0}(t) = x(t-t_0)\) et \(y_{t_0}(t) = y(t-t_0)\), alors :