Exercices sur feuille#
Exercice 1#
Calculez la série de Fourier du créneau \(x(t)\) tel que sur la période \([-T,\,T]\) il est défini comme :
\[\begin{split} x(t) = \begin{cases} A &\text{si}\, -\frac{T}{2} \leq t \leq \frac{T}{2}, \\ 0 &\text{sinon}. \end{cases} \end{split}\]Calculez la transformée de Fourier du signal \(y(t)\) :
\[\begin{split} y(t) = A\,\mathrm{rect}\left(\frac{t}{T}\right) = \begin{cases} A &\text{si}\, -\frac{T}{2} \leq t \leq \frac{T}{2}, \\ 0 &\text{sinon}. \end{cases} \end{split}\]Calculez la série de Fourier discrète du signal \(z[n]\) défini sur \(\{-N,\dots,\,N-1\}\) (avec \(N\) pair) :
\[\begin{split} z[n] = \begin{cases} A &\text{si}\, -\frac{N}{2} \leq n < \frac{N}{2}, \qquad\text{(attention :}\, z\left[\frac{N}{2}\right] = 0)\\ 0 &\text{sinon}. \end{cases} \end{split}\]
Exercice 2#
Calculez la série de Fourier d’une sinusoïde de fréquence \(f_0\) et de phase \(\varphi\).
Que devient le spectre lorsque la phase varie ?
Tracez le module et la phase de la série de Fourier pour \(\varphi=0\) (cas d’un sinus) et pour \(\varphi=+\pi/2\) (cas d’un cosinus). Que constatez-vous ?
Exercice 3#
Soit \(x(t)\) un signal réel. Quelle est la relation entre la transformée de Fourier de \(x(t)\) et celle de \(x(t)\times\cos(2\pi f_0 t)\) ?
Exercice 4#
Calculez la transformée de Fourier du signal \(x(t) = \exp(-at)\,u(t)\) où \(a\) est un réel strictement positif.
Exercice 5#
Le module du spectre d’un signal musical \(m(t)\) est schématisé ci-dessous (la phase n’a pas d’importance dans cet exercice) :
On envisage de transmettre ce signal par radio en modulation d’amplitude, c’est-à-dire de transmettre le signal \(x(t)\) défini par :
où \(f_p = 162\) kHz. Le deuxième terme de cette équation est la « porteuse » qui est modulée en amplitude par \(1+m(t)\).
À l’aide des propriétés de la transformée de Fourier, esquissez le module du spectre de \(x(t)\).
Une autre station de radio désire elle aussi transmettre un signal musical, dont la fréquence maximale est 8000 Hz. Proposez une valeur de la fréquence de la porteuse de ce deuxième programme.
Exercice 6#
Quel est, intuitivement, le spectre d’un signal temporel constant ?
En déduire le spectre d’une impulsion de Dirac centrée en 0.
Qu’en concluez-vous sur la composition fréquentielle d’une impulsion de Dirac ?
Exercice 7#
Le signal \(x(t)\) est représenté ci-dessous.
On note \(X(f)\) sa transformée de Fourier. Répondez aux questions suivantes sans calculer explicitement \(X(f)\).
\(X(f)\) est-elle périodique ? Si oui, donnez sa période.
\(X(f)\) est-elle un signal continu ou discret ?
Donnez la valeur de \(X(0)\).
Donnez \(\int|X(f)|^2\,df\)
Exercice 8#
Calculez la transformée de Fourier du signal
Exercice 9#
Calculez la transformée de Fourier du signal \(\mathrm{rect}(t)\times\cos(2\pi f_p t)\).
Exercice 10#
Le signal \(m(t)\) est à bande limitée : \(M(f)=0\) pour \(|f|>1\) kHz. Il est modulé en amplitude par une porteuse sinusoïdale de fréquence \(f_p=1\) kHz :
Sa démodulation est effectuée par le dispositif suivant :
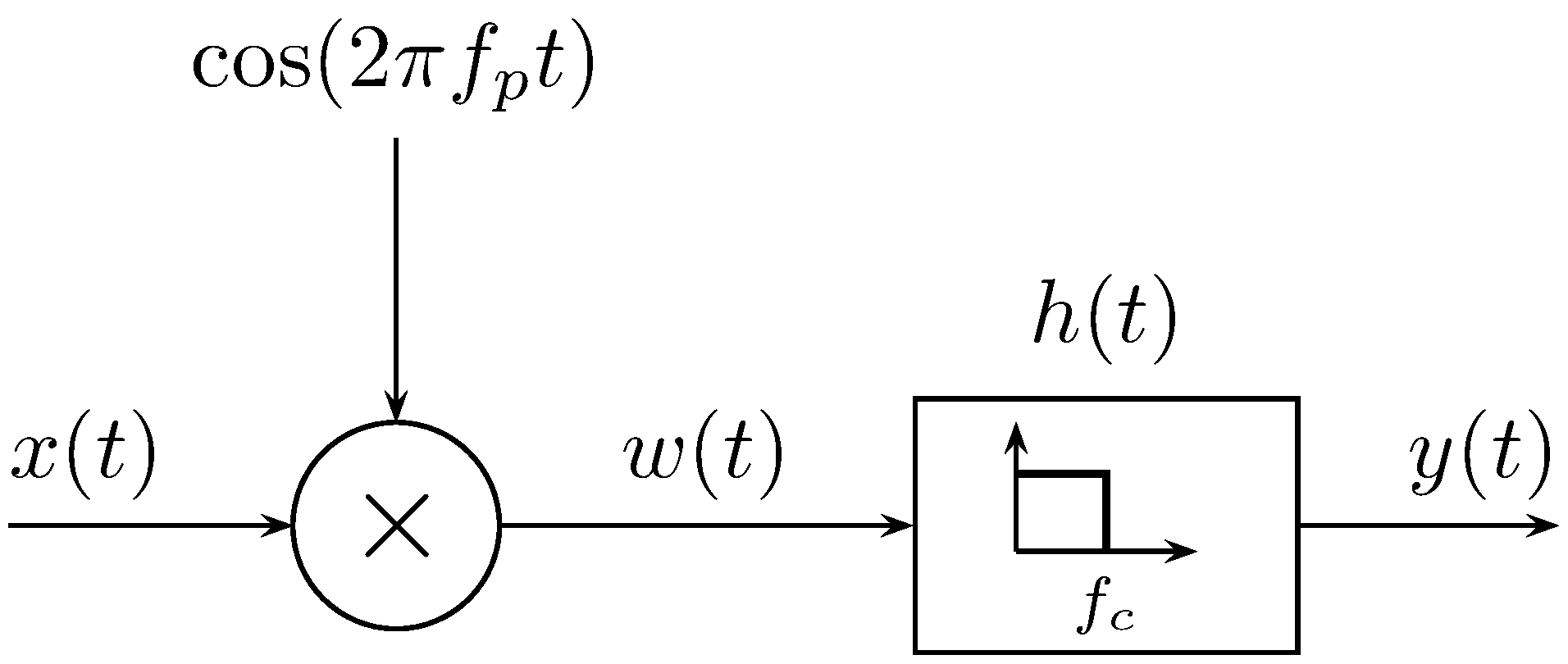
où le filtre passe-bas \(h(t)\) est idéal, de gain 2 et de fréquence de coupure \(f_c=1\) kHz. Déterminez \(y(t)\).
Exercice 11#
Lorsque Canal+ émettait encore en analogique, le son \(s(t)\) était chiffré en inversant son spectre comme schématisé ci-dessous. Proposez une technique pour réaliser cette opération.

Exercice 12#
La figure ci-dessous est tirée de la publication scientifique
R. Reiz, C. Gordan, D. Purcaru & C. Kokkonis, « Using Advanced Signal Processing Methods for DTMF Detection », Journal of Electrical and Electronics Engineering, 2009.
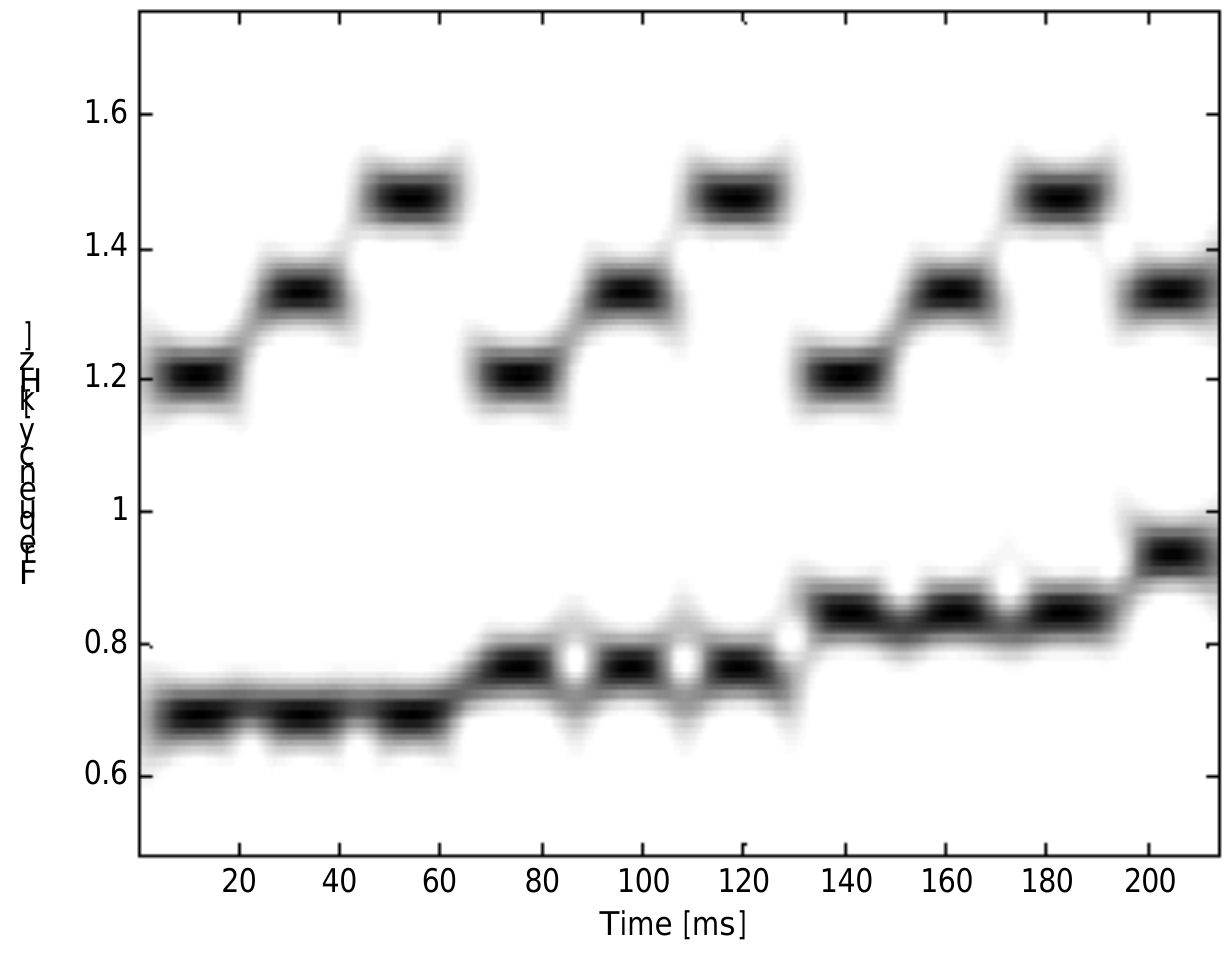
Que représente les axes (et oui, le titre de l’axe des ordonnées n’est pas clair : c’est une maladresse des auteurs…) ?
Décrivez précisément (en français ou sous forme mathématique) quel est le signal analysé.