Représentation vectorielle des signaux#
Un signal qui est échantillonné et à temps limité (c’est-à-dire nul ou non défini en dehors d’un intervalle) peut se représenter par une séquence finie de valeurs numériques. Dans le cas d’un signal \(x\) défini sur \(N\) échantillons, le signal est équivalent à un vecteur :
où les \(x_n\) sont les échantillons du signal. On notera \(x\in\mathbb{C}^N\) pour signifier que \(x\) est un signal échantillonné à temps limité de \(N\) échantillons à valeurs complexes.
Notez que, par convention, le premier échantillon est indexé par 0.
L’équivalence entre signal échantillonné à temps limité et vecteur a plusieurs intérêts :
on peut utiliser des outils de l’algèbre linéaire pour faire du traitement du signal ;
on peut faire des interprétations géométriques ;
c’est l’interprétation qui est faite dans les logiciels et les langages de calcul numérique, comme en Python.
Exemple
L’échelon \(u\) et l’impulsion \(\delta\) s’écrivent dont dans \(\mathbb{R}^2\) :
Leur représentation est donnée Fig. 9. Il s’agit simplement de signaux de deux échantillons. Les axes de cette représentation sont : les échantillons en abscisses, et les amplitudes en ordonnées.
Fig. 9 Représentation de l’échelon et de l’impulsion de taille 2 sous forme de signaux.#
La représentation vectorelle de ces deux signaux se fait dans un espace à deux dimensions, comme dans la Fig. 10. Les axes de cette représentation sont : le premier échantillon du signal en abscisse, et le deuxième échantillon en ordonnée.
Fig. 10 Représentation de l’échelon et de l’impulsion de taille 2 sous forme de vecteurs.#
Quelques définitions#
On peut définir les mêmes outils que ceux de la géométrie euclidienne pour les signaux échantillonnés à temps limité.
Produit scalaire#
Le produit scalaire entre deux signaux \(x\) et \(y\) de taille \(N\) est (la notation \(\cdot^*\) signifie conjugué) :
Orthogonalité#
Deux signaux sont orthogonaux si et seulement si leur produit scalaire est nul.
Norme#
La norme d’un signal \(x\) de taille \(N\) est :
Énergie#
L”énergie d’un signal de taille \(N\) est le carré de sa norme :
Distance#
La distance entre deux signaux \(x\) et \(y\) de taille \(N\) est la norme de la différence :
Erreur quadratique moyenne#
L”erreur quadratique moyenne (EQM) entre deux signaux \(x\) et \(y\) de taille \(N\) est :
Base#
Une base est un ensemble de \(N\) signaux tels que tout signal échantillonné de taille \(N\) peut s’écrire comme une combinaison linéaire unique de signaux de cette base. Ainsi, si \(\{\varphi_0,\, \varphi_1,\, \dots,\, \varphi_{N-1}\}\) est un ensemble de \(N\) signaux formant une base, alors tout signal \(x\in\mathbb{C}^N\) s’écrira
où les \(\alpha_k\) sont des coefficients uniques (il ne peut pas y avoir plusieurs jeux différents de coefficients \(\{\alpha_k\}\)).
Si en plus les vecteurs \(\{\varphi_k\}\) de cette base sont orthogonaux deux à deux et de norme 1, alors la base est orthonormée.
Exemple
Pour \(N=4\), les signaux \(\delta[n-k]\) avec \(k\in\{0,\dots,3\}\) forment une base, qui plus est orthonormée.
Fig. 11 Base canonique dans \(\mathbb{R}^4\).#
Nous ne représentons pas ces quatre signaux sous forme de vecteur, car cela nécessite de les représenter dans un espace à quatre dimensions (or, votre écran n’en a que deux).
Cette base est d’ailleurs appelée base canonique car c’est la base naturelle pour représenter les signaux. En effet, les échantillons de tout signal de taille \(N\) correspondent aux coefficients \(\alpha_k\).
Parfois, il est intéressant de représenter les signaux dans une autre base que la base canonique : on parle alors de décomposition ou de projection d’un signal \(x\) sur une base. La transformée de Fourier peut être vue comme la décomposition de signaux dans une autre base. De même, les techniques de compression (audio, image ou vidéo) utilisent astucieusement une décomposition dans une base particulière pour réduire le poids des données. Les coefficients du signal dans cette nouvelle base vont donc être différents des coefficients de la base canonique.
La décomposition d’un signal \(x\) de taille \(N\) dans une base orthonormée \(\{\varphi_k\}\), et donc le calcul des nouveaux coefficients \(\alpha_k\), s’obtient en calculant le produit scalaire de \(x\) avec chaque élément \(\varphi_k\) de la base :
La reconstruction du signal \(x\) consiste à réécrire le signal dans la base canonique depuis la base \(\{\varphi_k\}\). Pour cela, le signal \(x\) s’obtient par la somme des éléments de la base \(\varphi_k\) pondérés par les coefficients \(\alpha_k\) :
Un exemple de l’intérêt de la décomposition sur une base#
La compression d’un signal consiste à enregistrer ce signal en utilisant des techniques qui permettent de réduire sa place mémoire tout en conservant le maximum d’informations sur ce signal. Il existe deux familles de compression :
les techniques de compression sans perte permettent de gagner de la place mémoire sans modifier le signal, mais le gain en place mémoire est modéré ;
les techniques de compression avec perte permettent de gagner beaucoup de place mémoire, mais le signal sera nécessairement modifié. Tout l’enjeu consiste à trouver une technique qui permette de réduire le plus possible l’encombrement mémoire tout en garantissant une perte d’information du signal qui soit maîtrisée.
Dans cet exemple, nous allons montrer effectuer la compression avec perte d’un signal audio en utilisant sa décomposition dans une base appropriée : la base de Haar. Pour cela, nous considérons des signaux de taille \(N=16\).
Base de Haar#
Les 16 signaux \(\varphi_k\) (\(k\in\{0,\dots,N-1\}\)) de la base de Haar sont représentés ci-dessous.
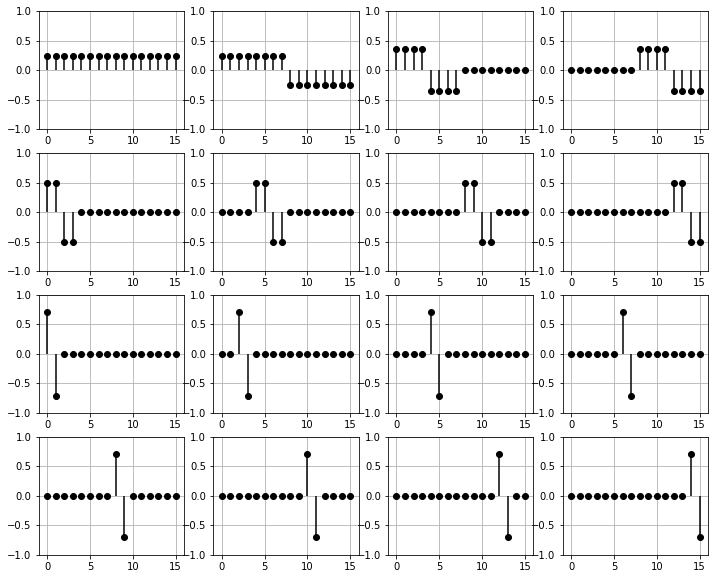
Décomposition d’un signal sur la base de Haar#
Considérons le signal \(x\) de taille \(N=16\) ci-dessous.
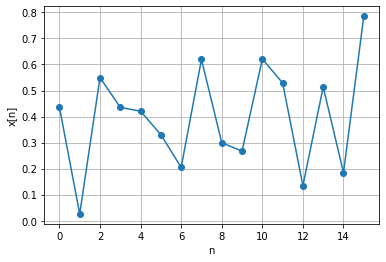
En utilisant le produit scalaire, on obtient les coefficients \(\alpha_k = \langle x, \varphi_k \rangle\) (\(k\in\{0,\dots,N-1\}\)) représentés ci-dessous :
[ 1.5890548 -0.07829068 -0.0451545 0.03493984 -0.26153187 -0.03660849
-0.29189699 -0.16080847 0.28996234 0.08085065 0.06366293 -0.29318226
0.02321248 0.06504798 -0.26799218 -0.42489713]
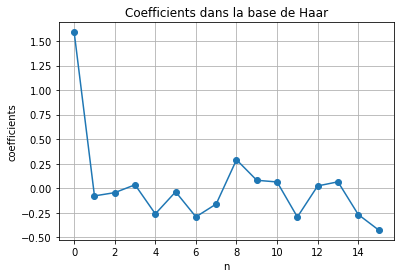
Compression du signal#
Dans cet exemple, nous allons considérer le cas d’une compression avec perte où l’on réduit de 50 % l’encombrement mémoire : le signal de 16 échantillons ne sera donc enregistré que sur 8 valeurs.
En restant dans la base canonique, on peut se contenter de supprimer les 8 échantillons les plus faibles du signal : ceux-ci sont donc mis à 0. Le signal reconstruit (donc en mettant des 0 à l’emplacement des échantillons supprimés) est représenté en orange. On peut calculer l’erreur quadratique moyenne avec le signal original \(x\) : elle est de 0,736.
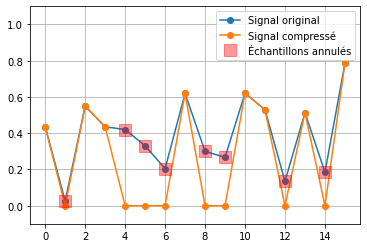
On peut faire la même chose mais en annulant la moitié des coefficients de la base de Haar : c’est donc les coefficients de la base qui sont enregistrés, et non les valeurs du signal. Le signal reconstruit est reconstruit à partir des coefficients de la base de Haar, en mettant à 0 ceux qui ont été supprimés. L’EQM du signal reconstruit est égale à 0,162.
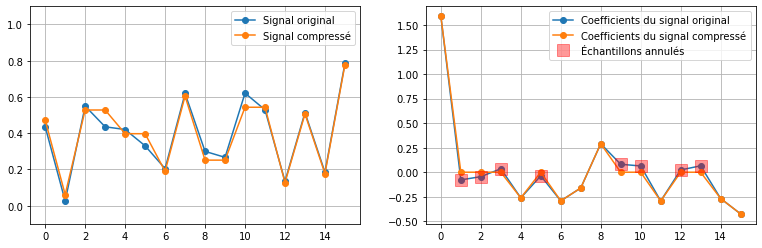
On remarque que l’EQM sur le signal reconstruit est beaucoup plus faible dans le cas où la compression est effectuée dans la base de Haar. L’erreur de reconstruction s’observe également sur le signal temporel : le signal compressé en passant dans la base de Haar est beaucoup plus proche que le signal compressé directement dans le domaine temporel. Cela illustre l’intérêt de changer de base pour effectuer une compression avec perte tout en limitant la perte d’information.
Application à un véritable signal audio#
La technique précédente a été appliquée sur un signal audio. Pour cela, le signal a été découpé en morceaux de 16 échantillons et un taux de compression de 50 % a été appliqué.
Musique originale :
Compression dans la base canonique :
Compression dans la base de Haar :