Transformations de Fourier

Joseph Fourier (1768–1830) était professeur à l’École Polytechnique, scientifique pendant la campagne de Napoléon en Égypte, et préfet de l’Isère. Il a aussi été membre de l’Académie des sciences et de l’Académie française.

En travaillant sur le phénomène de propagation de la chaleur, il s’aperçut qu’il était utile de représenter la distribution de température dans les matériaux comme une somme de sinusoïdes : c’est ce qu’on appelle maintenant une décomposition en série de Fourier. La série de Fourier, et les autres transformations qui en découlent, jouent un rôle capital en traitement du signal car elles permettent de mettre en évidence les fréquences contenues dans un signal.

La vidéo ci-dessous raconte la vie de Joseph Fourier.

Cette autre vidéo se concentre sur les applications actuelles des transformations de Fourier.

Il existe quatre transformations de Fourier, chacune adaptée au type de signal considéré :

• la « série de Fourier » (SF) s’applique aux signaux à temps continu et périodiques,

• la « transformée de Fourier » (TF) s’applique aux signaux à temps continu et apériodiques,

• la « série de Fourier discrète » (SFD) s’applique aux signaux à temps discret et périodiques,

• et la « transformée de Fourier à temps discret » (TFTD) s’applique aux signaux à temps discret et apériodiques.

Série de Fourier

Tout signal \(x(t)\) à temps continu et périodique de période \(T\) peut s’écrire comme une combinaison linéaire de fonctions \(\exp\left(j 2\pi k t/T\right)\), qui sont elles-mêmes périodiques de période \(T\) :

Cette formule est la série de Fourier inverse.

\[ x(t) = \sum_{k=-\infty}^{+\infty} X[k] e^{+j 2 \pi k t / T} \]

Vous remarquerez que le signal temporel \(x\) est noté en minuscule, alors que le signal fréquentiel \(X\) est en majuscule.

où \(k \in \mathbb{Z}\) est la « fréquence » et \(X[k]\) sont des coefficients. L’ensemble de ces coefficients, noté simplement \(X\), est la série de Fourier de \(x\) ; c’est aussi un signal. On montre que les coefficients de la série de Fourier sont définis par :

Cette formule est la série de Fourier.

\[ X[k] = \frac{1}{T} \int_T x(t) e^{-j 2 \pi k t / T } dt. \]

Le terme \(k\) est appelé la \(k\)^e harmonique. En particulier, le terme \(X[1]\) est la première harmonique, que l’on appelle aussi la « composante fondamentale ». Le terme \(X[0]\) correspond à la moyenne du signal :

\[ X[0] = \frac{1}{T} \int_T x(t) dt. \]

Formulation alternative

Parfois, la série de Fourier de signaux réels est définie comme l’ensemble des coefficients \(a_k\) et \(b_k\) tels que :

\[\begin{split} a_0 &= \frac{1}{T} \int_0^T x(t) dt \\ \forall k \in\mathbb{N}^*, \qquad a_k &= \frac{2}{T} \int_0^T x(t) \cos(2 \pi k t / T) dt \\ \forall k \in\mathbb{N}^*, \qquad b_k &= \frac{2}{T} \int_0^T x(t) \sin(2 \pi k t / T) dt \end{split}\]

La relation entre ces coefficients \(a_k\) et \(b_k\) avec l’expression précédente de la série de Fourier est :

\[\begin{split} \text{si}\, k<0\,:\qquad X[k] &= \frac{a_{-k}+jb_{-k}}{2} \\ \text{si}\, k=0\,:\qquad X[0] &= a_0 \\ \text{si}\, k>0\,:\qquad X[k] &= \frac{a_k-jb_k}{2} \end{split}\]

et la formule de la série de Fourier inverse devient :

\[ x(t) = a_0 + \sum_{k=1}^{+\infty} \left( a_k \cos(2 \pi k t / T) + b_k \sin(2 \pi k t / T) \right). \]

Dans le cadre de ce module, nous n’utiliserons pas les formules faisant intervenir \(a_k\) et \(b_k\) car elles obligent à effectuer deux fois plus de calculs qu’avec les formules précédentes utilisant \(X[k]\). En effet, la formulation avec l’exponentielle complexe regroupe les termes en cosinus et en sinus. C’est donc plus simple en complexe ! 😜

Transformée de Fourier

On peut considérer qu’un signal apériodique est le cas limite d’un signal périodique de période infinie. Dans ce cas, la série de Fourier tend vers la transformée de Fourier :

Cette formule est la transformée de Fourier.

\[ X(f) = \int_{-\infty}^{+\infty} x(t) e^{-j 2 \pi f t} dt \]

où \(f\in\mathbb{R}\) est la fréquence. De même qu’avec la série de Fourier, le signal temporel \(x\) peut être reconstruit à partir de \(X\) :

Cette formule est la transformée de Fourier inverse.

\[ x(t) = \int_{-\infty}^{+\infty} X(f) e^{+j 2 \pi f t} df. \]

Série de Fourier discrète

De même que pour la série de Fourier, un signal à temps discret et périodique de période \(N\) peut s’écrire comme la combinaison linéaire de fonctions \(\exp\left(j\frac{2\pi k n}{N}\right)\), qui sont également périodiques de période \(N\) :

Cette formule est la série de Fourier discrète inverse.

\[ x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{+j 2 \pi k n / N} \]

et :

Cette formule est la série de Fourier discrète.

\[ X[k] = \sum_{n=0}^{N-1} x[n] e^{-j 2 \pi k n / N}. \]

Remarque   Un signal \(x[n]\) à durée limité (donc non défini en dehors de l’intervalle \(\{0,\dots,N-1\}\)) peut être vu comme un signal périodique de période \(N\). Il possède donc une série de Fourier discrète qui s’appelle dans ce cas « transformée de Fourier discrète » (TFD). Comme les signaux que l’on traite sur ordinateur sont toujours à durée limitée, alors ce sera cette transformée de Fourier discrète qui sera calculée. Il existe un algorithme très rapide pour la calculer : l’algorithme FFT (implémenté en Python dans la fonction numpy.fft.fft).

Représentation

On l’a vu, les transformations de Fourier \(X\) du signal \(x\) sont des signaux. En raison de l’exponentielle complexe dans les formules ci-dessus, \(X\) est souvent complexe. Pour représenter \(X\), il faudrait donc se placer dans un espace en trois dimensions dont les axes seraient la fréquence (\(f\) ou \(k\)), la partie réelle de \(X\) et la partie imaginaire de \(X\). Vous conviendrez que ce n’est pas commode de représenter un signal à valeurs complexes sur une feuille ou un écran…

Pour cette raison, les transformations de Fourier sont représentées à l’aide de deux graphiques :

• le premier représente le module de \(X\) en fonction de la fréquence,

• le second représente l’argument de \(X\) en fonction de la fréquence.

L’ensemble de ces deux graphiques s’appelle le « spectre ».

Fig. 13 Spectre de la transformée de Fourier de \(3\,\mathrm{rect}(t+1/4)\).

On peut être surpris que le spectre présente des fréquences « négatives » (à gauche de l’axe des ordonnées). En fait, il ne s’agit pas de fréquences négatives (cela n’a pas de sens), mais d’exponentielles complexes tournant en sens opposé aux exponentielles complexes de la partie à droite de l’axe des ordonnées.

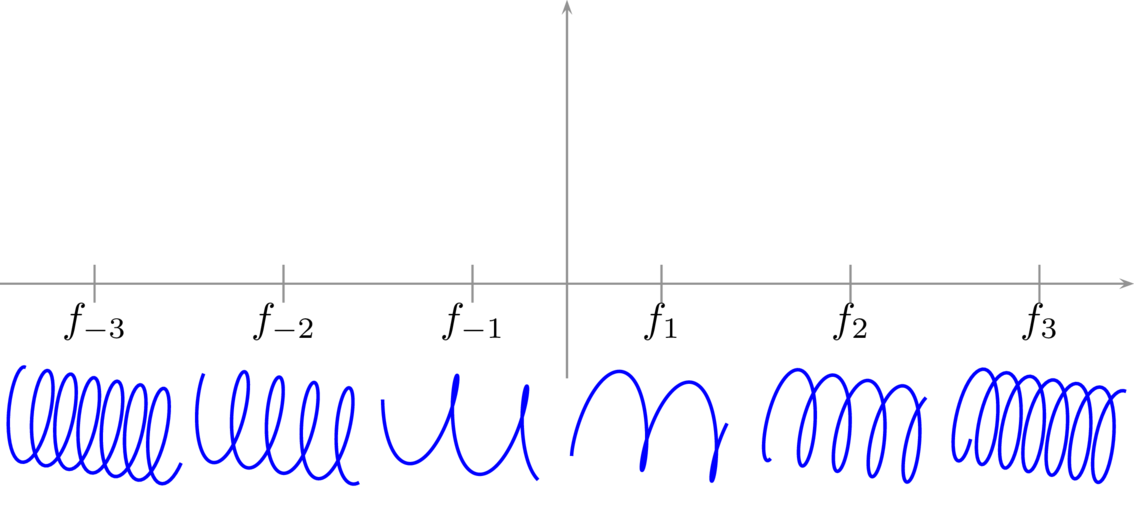
Fig. 14 Illustration des exponentielles complexes associées à l’axe des fréquences d’un spectre.

Récapitulatif

Quelle que soit la transformation, on peut donc résumer ainsi les différentes notations utilisées :

Domaine :		temporel	\(\quad\xrightarrow{\;\mathcal{F}\;}\quad\)	fréquentiel
Signal :		\(x\)	\(\quad\xrightarrow{\;\mathcal{F}\;}\quad\)	\(X\)
Variable :		\(t\) ou \(n\)	\(\quad\xrightarrow{\;\mathcal{F}\;}\quad\)	\(f\) ou \(k\)
Exemple d'unité :		seconde (s)	\(\quad\xrightarrow{\;\mathcal{F}\;}\quad\)	s–1 = hertz (Hz)

Par ailleurs, on remarque que le passage du domaine temporel au domaine fréquentiel utilise une exponentielle du type \(e^{-\theta}\) alors que l’inverse utilise \(e^{+\theta}\) où :

• \(\theta = j 2 \pi k t / T\) pour la SF,

• \(\theta = j 2 \pi f t \) pour la TF,

• \(\theta = j 2 \pi k n / N\) pour la SFD (ou TFD).

On retrouve donc toujours le même schéma pour \(\theta\) :

\[ \theta = j 2 \pi \times \text{fréquence} \times \text{temps} \times \text{période éventuelle} \]

Avertissement

\(t\) et \(f\) sont les variables de temps et de fréquence, respectivement. En revanche, \(T\) et son inverse \(F=1/T\) sont des constantes représentant la période et la fréquence d’un signal, respectivement. Ne confondez pas la fréquence \(f\) qui est une variable dont dépend \(X\) et la fréquence \(F\) qui est une constante représentant la fréquence d’un signal périodique \(x\) !