Exercices sur feuille

Exercices sur feuille#

Exercice 1#

  • Montrez que le train d’impulsions \(x^*\) défini par

    \[\begin{split} x^*(t) = \begin{cases} x(t) &\text{si}\ t\ \text{est multiple de}\ T_e \\ 0 &\text{sinon}, \end{cases} \end{split}\]

    où \(x\) est un signal analogique, s’écrit comme le produit d’un signal avec un train d’impulsions \(Ш\) dont la période est à déterminer.

  • Montrez que \(x^*\) a pour transformée de Fourier

    \[ X^*(f) = f_e \sum_k X(f-kf_e). \]

    La transformée de Fourier de \(Ш_T(t)\) est \(\frac{1}{T} Ш_{1/T}(f)\).

Exercice 2#

Rappelez les relations entre fréquence d’échantillonnage, période d’échantillonnage et fréquence de Nyquist.

Exercice 3#

Proposez une fréquence d’échantillonnage pour effectuer un enregistrement numérique d’un électrocardiogramme.

Exercice 4#

Une sinusoïde \(x(t)\) de fréquence 10 kHz est échantillonnée à une fréquence de 8 kHz. Quel sera le signal analogique reconstruit à partir du signal numérique ?

Exercice 5#

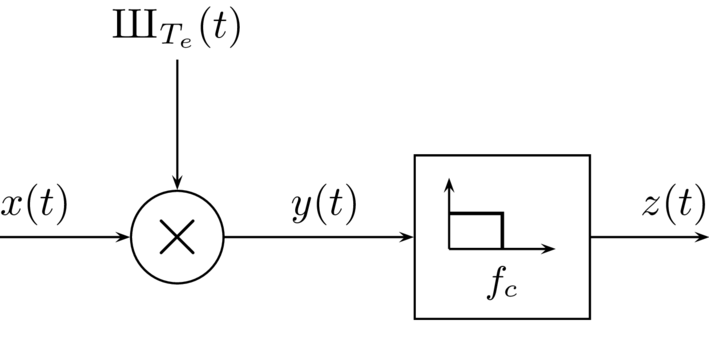
Pour étudier l’effet du repliement spectral, on applique la chaîne de traitement ci-dessous à un signal sinusoïdal : le signal \(x(t) = \cos(2\pi f_0 t)\) est échantillonné à une fréquence \(f_e=1/T_e\) pour obtenir le signal \(y(t)\), puis filtré par un filtre passe-bas idéal de fréquence de coupure \(f_c = f_e/2\) pour obtenir le signal \(z(t)\).

../_images/aliasing.png

Dans un premier temps, on prend \(f_0=2\) kHz et \(f_e=6\) kHz.

  • Représentez les modules des spectres de \(x(t)\), \(y(t)\) et \(z(t)\).

  • Comparez le signal \(z(t)\) avec \(x(t)\). Y a-t-il du repliement spectral ?

  • Mêmes questions avec \(f_e = 3\) kHz.

Exercice 6#

Le signal \(x(t) = A \sin(2 \pi f t + \varphi)\) avec \(A=3\), \(f=2\) Hz et \(\varphi=\pi/5\) est quantifié sur 8 bits avec un quantifieur uniforme par arrondi. Quel valeur du pas de quantification doit-on choisir pour obtenir la meilleure résolution sans saturation ?

Exercice 7#

Sur un CD audio, le signal sonore est quantifié sur 16 bits.

  • Déterminez le nombre de niveaux de quantification.

  • En supposant le signal sonore comme une sinusoïde d’amplitude \(A\), quelle est la valeur maximale de l’erreur ?

  • Comparez la puissance de l’erreur à la puissance du signal.

Exercice 8#

Un signal analogique de bande passante 20 kHz est numérisé sur 16 bits. Combien de bits par seconde au minimum doit traiter le convertisseur analogique-numérique ? En déduire la capacité de stockage d’un CD audio de 60 minutes, sachant que le son y est enregistré en stéréo.

Exercice 9#

Un convertisseur numérique-analogique 5 bits produit des tensions positives (commençant à 0 mV). Une entrée égale à 1 0 1 0 0 (bit de poids fort à gauche) correspond à une tension de 100 mV.

  • Calculez le pas de quantification (résolution) du convertisseur.

  • Calculez la tension maximale (pleine échelle) du convertisseur.

  • Quelle tension correspond à une entrée égale à 1 1 1 0 1 ?

Contenu