Registration

Image registration is the process of applying geometric transformation on images so that they lie in the same coordinate system. Registration has many applications, for instance in remote sensing (Fig. 58), medical imaging (Fig. 59), or photograph stitching (Fig. 60).

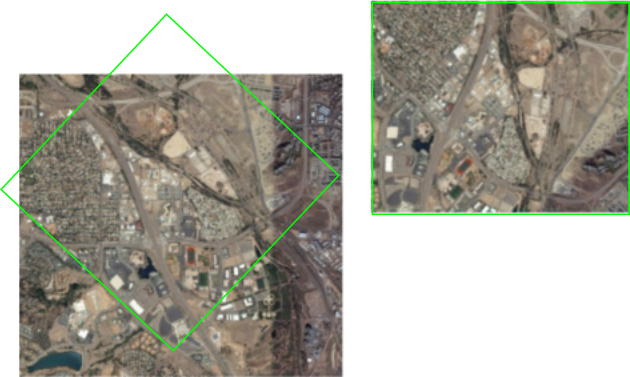
Fig. 58 Registration of remote sensing images.

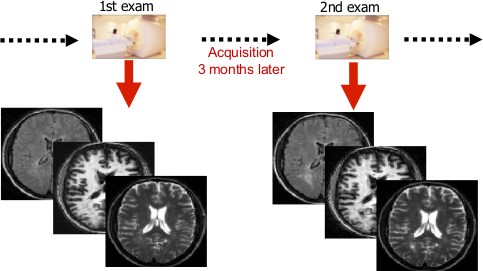
Fig. 59 Change detection in medical imaging.

Fig. 60 Photograph stitching.

The pipeline of image registration is given in Fig. 61. The next sections are devoted to give details on each step.

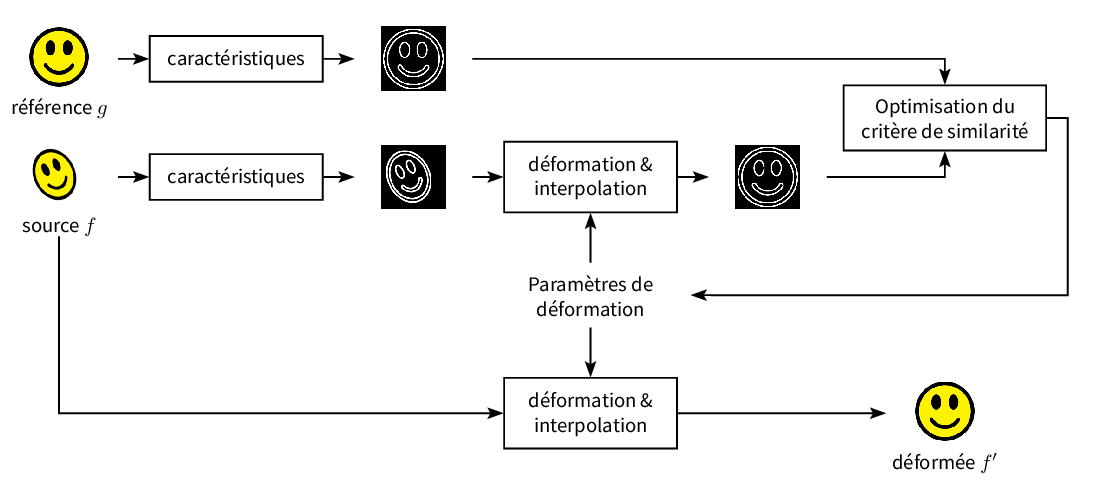
Fig. 61 Image registration. In this example, the characteristics are the edges, but they can be other informations like keypoints.

Image characteristics

La déformation à appliquer sur l’image source est basée sur des caractéristiques de cette image. Le choix des caractéristiques utilisées conduit à l’une des deux méthodes de recalage décrite ci-après.

Approche iconique

L’approche iconique (intensity-based registration) se base directement sur l’intensité des pixels de l’image. Ainsi, toute l’information contenue dans l’intensité des pixels est utilisée. À la place de l’image elle-même, on peut aussi utiliser une de ses transformations (Fourier, ondelette, gradient…).

L’avantage de l’approche iconique est quelle est relativement bien automatisée.

Les inconvénients de l’approche iconique sont le coût calculatoire important et la mémoire nécessaire, mais elle est également sensible au bruit et aux variations d’intensité entre les images.

Approche géométrique

Dans l’approche géométrique (feature-based registration), la déformation à appliquer à l’image source n’est pas définie à partir des intensités des pixels, mais à partir de caractéristiques particulières de l’image. Ces primitives peuvent être :

• intrinsèques à l’image : on se base sur les coins, les contours des objets, etc.

• extrinsèques à l’image : on se base sur des marqueurs insérés sur les objets. Il faut ensuite apparier les primitives (feature matching).

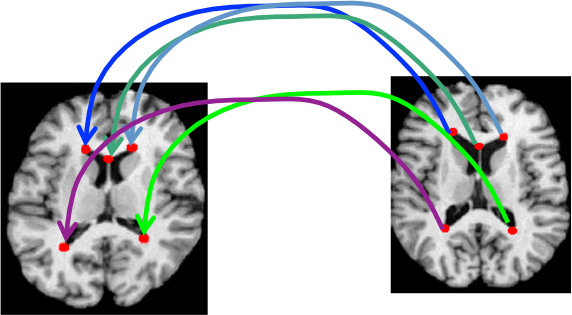
Fig. 62 Appariement de primitives entre deux images.

Les avantages de l’approche géométrique sont d’utiliser peu de données de l’image, impliquant un coût calculatoire faible.

Les inconvénients de l’approche géométrique sont que :

• l’appariement des primitives peut être difficile à effectuer,

• la qualité du recalage dépend de la précision de l’extraction des primitives,

• la précision du recalage n’est garantie qu’au voisinage des primitives.

Transform model

La déformation appliquée à l’image source est une transformation mathématique qui peut être linéaire ou non.

Une transformation linéaire s’écrit :

\[ p' = M p \]

où

• \(p = [x \; y \; 1]^T\) regroupe les coordonnées du pixel \((x,y)\) de l’image source,

• \(p' = [x' \; y' \; 1]^T\) regroupe les coordonnées du pixel \((x',y')\) de l’image déformée,

• \(M \in \mathbb{R}^{3\times3}\) est la matrice de transformation.

Par exemple, si la matrice de déformation est

\[\begin{split} M = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

alors

\[\begin{split} p' = \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix} \end{split}\]

Les coordonnées du pixel \(p'\) de l’image transformée correspondent à celle du pixel \(p\) de l’image source après une translation de de \(t_x\) pixels en \(x\) et \(t_y\) pixels en \(y\).

Note

Notez que la définition de \(p'\) à partir de \(p\) peut résulter en une image transformée composée de pixels vides si aucun pixel \(p\) de l’image originale \(f\) ne tombe sur un pixel \(p'\) de l’image transformée \(f'\). Pour éviter cela et obtenir la valeur de tous les pixels \(p'\), on applique l’inverse de la transformation pour trouver la coordonnée (souvent non entière) dans l’image originale \(f\). Une interpolation permet de déterminer la valeur de cette coordonnée, et donc du pixel \(p'\).

Les différents types de déformations sont illustrés ci-après sur l’image représentée Fig. 63.

Fig. 63 Image Lena.

Déformation rigide

Une déformation rigide (ou euclidienne) est une transformation linéaire définie avec 3 paramètres : \(\theta=\{\alpha,t_x,t_y\}\). La déformation rigide regroupe donc une rotation d’angle \(\alpha\) et une translation \((t_x,t_y)\). La matrice de déformation s’écrit :

\[\begin{split} M\!=\!\begin{pmatrix} \cos\alpha & \sin\alpha & t_x \\ -\sin\alpha & \cos\alpha & t_y \\ 0 & 0 & 1 \end{pmatrix} \end{split}\]

Fig. 64 Exemple de déformation rigide.

Déformation affine

Une déformation affine est une transformation bilinéaire définie avec 6 paramètres : \(\theta=\{m_{11}, m_{12}, m_{13}, m_{21}, m_{22}, m_{23}\}\). L’image subit une mise à l’échelle et un cisaillement : les droites parallèles restent parallèles après déformation, mais les angles changent. La matrice de déformation s’écrit :

\[\begin{split} M\!=\!\begin{pmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ 0 & 0 & 1 \end{pmatrix} \end{split}\]

Fig. 65 Exemple de déformation affine.

Déformation perspective

Une déformation perspective est une transformation linéaire définie avec 9 paramètres : \(\theta=\{m_{11}, m_{12}, m_{13}, m_{21}, m_{22}, m_{23}, m_{31}, m_{32}, m_{33}\}\). La matrice de déformation s’écrit :

\[\begin{split} M\!=\!\begin{pmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{pmatrix} \end{split}\]

Fig. 66 Déformation perspective.

Déformation non linéaire

On peut définir tout autre type de déformation sans passer par une transformation linéaire. Ainsi, l’utilisation de fonctions 2D spécifiques (polynôme, sinusoïde, spline, ondelette…) ou d’un champ de déformation non paramétrique est envisageable.

Il peut alors être nécessaire d’introduire des contraintes sur le modèle de déformation (préservation de la topologie, douceur, symétrie…).

Fig. 67 Déformation non linéaire.

Interpolation and similarity criterion

Connaissant les paramètres de déformation \(\theta\) à appliquer sur l’image, la transformation correspondante peut être effectuée. Il s’agit d’un problème d’interpolation.

Le critère de similarité (error metric) \(E(\theta)\) représente la distance (au sens mathématique) entre l’image de référence \(g\) et l’image déformée \(f'\) (obtenue an appliquant le modèle de déformation de paramètres \(\theta\) sur l’image source \(f\)). Cette distance est minimale lorsque les deux images se superposent au mieux, c’est-à-dire lorsque la similarité entre l’image de référence \(g\) et l’image déformée \(f\,'\) est maximale.

L’objectif du recalage est de trouver les paramètres \(\theta\) qui minimisent le critère de similarité \(E(\theta)\) : c’est donc un problème d’optimisation. Le choix de \(E\) dépend quant à lui du choix de l’approche choisie.

Approche iconique

Dans le cas d’une approche iconique (basée sur l’intensité des pixels), on utilisera un critère de similarité dit dense. Il existe plusieurs hypothèses sur les liens entre les intensités des deux images. Dans le cas le plus simple, on suppose que les intensités des pixels sont égales à un bruit additif gaussien près, donc le critère de similarité peut être la distance euclidienne, qui est proportionnelle à l’erreur quadratique moyenne (EQM) :

\[ E(\theta) = \sum_{m=1}^M \sum_{n=1}^N \big(f\,'(m,n) - g(m,n)\big)^2 \]

Aapproche géométrique

Dans le cas d’une approche géométrique (basée sur des caractéristiques), on utilisera une distance entre ces primitives.

• Par exemple, dans le cas où les primitives sont des pixels particuliers, on peut considérer la distance entre ces pixels avec la norme euclidienne :

  \[ E(\theta) = \sum_{n=1}^N (x_n-x'_n)^2 + (y_n-y'_n)^2 \]

  où \((x_n,y_n)\) et \((x'_n,y'_n)\) sont les coordonnées des pixels appariés.

• Un autre exemple est le cas où les primitives sont des courbes. L’algorithme ICP (Iterative Closest Point) peut être utilisé pour déterminer une distance entre ces deux courbes, définie comme

  \[ E(\theta) = \sum_{n=1}^N d_n^2 \]

  où \(d_n\) est la distance entre chaque point de la courbe 1 avec le point le plus proche de la courbe 2.

  

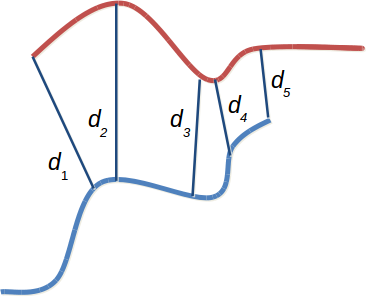
  Fig. 68 Distance entre deux courbes avec l’algorithme ICP.

Optimisation du critère de similarité

Comme on l’a dit précédemment, on cherche les valeurs des paramètres \(\theta\) de la transformation qui minimise \(E(\theta)\). Mathématiquement, le problème s’écrit :

\[ \hat{\theta} = \arg \min_{\theta} E(\theta) \]

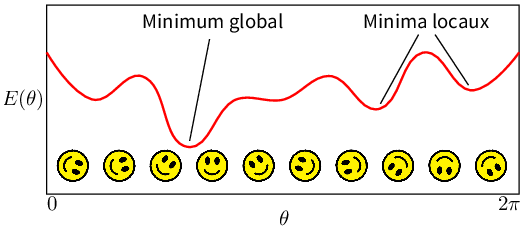
Fig. 69 Principe de l’optimisation d’un critère \(E\) : exemple pour \(\theta=\alpha\) dans le cas d’une simple rotation.

Il existe énormément de méthodes d’optimisation dont la description dépasse le cadre de ce cours :

• Solution explicite (en annulant la dérivée de \(E\)),

• Recherche exhaustive (toutes les possibilités sont testées),

• Méthodes déterministes : algorithme du simplexe, descente de gradient, gradient conjugué, algorithme de Levenberg-Marquardt, etc.

• Méthodes stochastiques : recuit simulé, algorithmes génétiques, gradient stochastique, etc.

On peut combiner ces méthodes d’optimisation avec des schémas hiérarchiques (hierarchical / coarse to fine approaches) : l’idée est de décomposer le problème initial en plusieurs petits problèmes de complexité moindre. Cela a tendance à réduire le risque de convergence vers un minimum local et à accélérer le calcul. On peut donc utiliser une approche par multi-résolution (on commence par effectuer l’optimisation sur une image très sous-échantillonnée et affiner l’optimisation à des échelles progressivement plus proches de l’image originale). On peut également, en particulier dans le cas d’un modèle de déformation complexe, commencer par optimiser un modèle simple (déformation rigide par exemple) puis le complexifier petit à petit.